山东省济南市历城区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
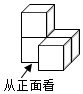
1. 如图是由4个相同的小正方体组成的一个立体图形,其主视图是( )
 A、
A、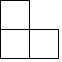 B、
B、 C、
C、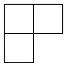 D、
D、 2. 在Rt△ABC中,∠C=90°,AB=13,AC=12,则sinB的值是A、 B、 C、 D、3. 将二次函数的图象平移后,得到二次函数的图象,平移的方法可以是( )A、向左平移1个单位长度 B、向右平移1个单位长度 C、向上平移1个单位长度 D、向下平移1个单位长度4. 如图,正方形ABCD中,点E是对角线AC上的一点,且连接DE,则∠CDE的度数为( )
2. 在Rt△ABC中,∠C=90°,AB=13,AC=12,则sinB的值是A、 B、 C、 D、3. 将二次函数的图象平移后,得到二次函数的图象,平移的方法可以是( )A、向左平移1个单位长度 B、向右平移1个单位长度 C、向上平移1个单位长度 D、向下平移1个单位长度4. 如图,正方形ABCD中,点E是对角线AC上的一点,且连接DE,则∠CDE的度数为( ) A、20° B、22.5° C、25° D、30°5. 在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同,小明通过多次试验发现,摸出红球的频率稳定在0.6左右,则袋子中红球的个数最有可能是( )A、5 B、8 C、12 D、156. 如图,在△ABC中, , , , , 则AB的值为( )
A、20° B、22.5° C、25° D、30°5. 在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同,小明通过多次试验发现,摸出红球的频率稳定在0.6左右,则袋子中红球的个数最有可能是( )A、5 B、8 C、12 D、156. 如图,在△ABC中, , , , , 则AB的值为( ) A、6 B、8 C、9 D、127. 如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为375平方米的矩形临时仓库,仓库一边靠墙,另外三边用总长为55米的栅栏围成,若设栅栏AB的长为x米,则下列各方程中,正确的是( )
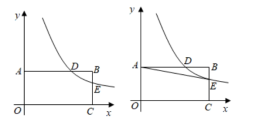
A、6 B、8 C、9 D、127. 如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为375平方米的矩形临时仓库,仓库一边靠墙,另外三边用总长为55米的栅栏围成,若设栅栏AB的长为x米,则下列各方程中,正确的是( ) A、x(55﹣x)=375 B、x(55﹣2x)=375 C、x(55﹣2x)=375 D、x(55﹣x)=3758. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )
A、x(55﹣x)=375 B、x(55﹣2x)=375 C、x(55﹣2x)=375 D、x(55﹣x)=3758. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )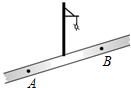 A、
A、 B、
B、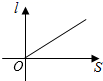 C、
C、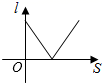 D、
D、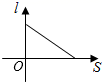 9. 如图,等边三角形 内接于 ,若 的半径为2,则图中阴影部分的面积等于( )
9. 如图,等边三角形 内接于 ,若 的半径为2,则图中阴影部分的面积等于( ) A、 B、 C、 D、10. 如图,在直角坐标系中,的边OB在y轴上, , , 点C在AB上, , 且 , 若双曲线经过点C,则k的值为( )
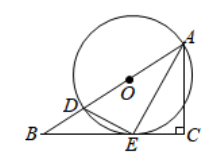
A、 B、 C、 D、10. 如图,在直角坐标系中,的边OB在y轴上, , , 点C在AB上, , 且 , 若双曲线经过点C,则k的值为( )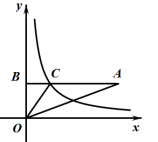 A、 B、 C、1 D、211. 如图,某建筑物的顶部有一块宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,米,米,则宣传牌CD的高度是( )米
A、 B、 C、1 D、211. 如图,某建筑物的顶部有一块宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,米,米,则宣传牌CD的高度是( )米 A、 B、 C、 D、12. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线 . 下列结论:①:②;③;④ . 正确的有( )
A、 B、 C、 D、12. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线 . 下列结论:①:②;③;④ . 正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 若
14. 若关于x的一元二次方程有两个不相等实数根,则实数a的取值范围是 .15. 某中学举办庆祝中国共产党建党100周年党史知识竞赛.某班有5名学生报名,其中2男3女,计划从这5名学生中随机抽选两名学生参加知识竞赛,所选两名学生中恰好1男1女的概率为 .16. 如图,在菱形ABCD中,E,F,G分别是AD,AB,CD的中点,且 , , 则菱形ABCD的面积是 . 17. 如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,点O、A、B、C均在格点上,则过A、B、C三点的圆的圆心坐标为 .
17. 如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,点O、A、B、C均在格点上,则过A、B、C三点的圆的圆心坐标为 . 18. 如图,在矩形ABCD中, , , 点E,F分别在边AD,BC上,且 , 沿直线EF翻折,点A的对应点恰好落在对角线AC上,点B的对应点为;分别在线段EF,上取点M,N,沿直线MN二次翻折,使点F与点E重合,则线段MN的长为 .
18. 如图,在矩形ABCD中, , , 点E,F分别在边AD,BC上,且 , 沿直线EF翻折,点A的对应点恰好落在对角线AC上,点B的对应点为;分别在线段EF,上取点M,N,沿直线MN二次翻折,使点F与点E重合,则线段MN的长为 .
三、解答题
-
19. 计算: .20. 解方程: .21. 已知:如图,矩形ABCD中,对角线AC与BD相交于点E,作 , , CF与DF相交于点F.求证:四边形DECF为菱形.
 22. 某社区为了调查居民第三季度的用电情况,随机抽取了小区20户居民的用电量进行调查.数据如下:(单位:度)
22. 某社区为了调查居民第三季度的用电情况,随机抽取了小区20户居民的用电量进行调查.数据如下:(单位:度)670,870,730,1140,700,690,1170,970,1000,970
730,840,1060,870,720,870,1060,930,840,870
整理数据:按如下分段整理样本数据并补至表格(表1)
用电量x(度)
人数
a
6
b
4
分析数据:补全下列表格中的统计量(表2)
平均数
中位数
众数
885
c
d
得出结论:
(1)、表中的a= , b= , c= , d= .(2)、若将表1中的数据制作成一个扇形统计图,则所表示的扇形圆心角的度数为度.(3)、如果该小区有住户400户,请根据样本估计用电量在的居民户数.23. 一家商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售、增加盈利,该店采取降价措施,在每件盈利不少于24元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、求每件商品降价多少元时,该商店每天销售利润为1200元.(2)、求每件商品降价多少元时,该商店每天销售利润最大,最大利润是多少元?