山东省济南市莱芜区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 如图所示的几何体的左视图为( )
 A、
A、 B、
B、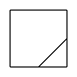 C、
C、 D、
D、 2. 下列函数中,随的增大而减小的函数是( )A、 B、 C、 D、3. 在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )A、 B、 C、 D、4. 如图,给出了一种机器零件的示意图,其中米,米,则( )
2. 下列函数中,随的增大而减小的函数是( )A、 B、 C、 D、3. 在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )A、 B、 C、 D、4. 如图,给出了一种机器零件的示意图,其中米,米,则( )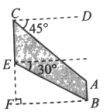 A、米 B、米 C、米 D、米5. 如图,是半圆的直径,、是半圆上的两点, , 则( )
A、米 B、米 C、米 D、米5. 如图,是半圆的直径,、是半圆上的两点, , 则( )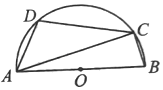 A、55° B、65° C、75° D、85°6. 将抛物线的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )A、 B、 C、 D、7. 如图,某水库大坝的横断面是梯形 , 坝高 , 斜坡的坡比为 , 则斜坡BC=( )
A、55° B、65° C、75° D、85°6. 将抛物线的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )A、 B、 C、 D、7. 如图,某水库大坝的横断面是梯形 , 坝高 , 斜坡的坡比为 , 则斜坡BC=( )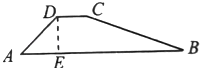 A、13m B、8m C、18m D、12m8. 如图,的半径为6,将劣弧沿弦翻折,恰好经过圆心 , 点为优弧上的一个动点,则面积的最大值是( )
A、13m B、8m C、18m D、12m8. 如图,的半径为6,将劣弧沿弦翻折,恰好经过圆心 , 点为优弧上的一个动点,则面积的最大值是( )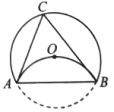 A、 B、 C、 D、9. 如图,过轴正半轴上的任意点 , 作轴的平行线,分别与反比例函数和的图象交于、两点.若点是轴上任意一点,则的面积为( )
A、 B、 C、 D、9. 如图,过轴正半轴上的任意点 , 作轴的平行线,分别与反比例函数和的图象交于、两点.若点是轴上任意一点,则的面积为( ) A、4 B、3 C、2 D、110. 用一块弧长的扇形铁片,做一个高为4cm的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为( )A、 B、 C、 D、11. 一次函数与二次函数在同一平面直角坐标系中的图象可能是( )A、
A、4 B、3 C、2 D、110. 用一块弧长的扇形铁片,做一个高为4cm的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为( )A、 B、 C、 D、11. 一次函数与二次函数在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 12. 如图是抛物线的部分图象,图象过点 , 对称轴为直线 , 有下列五个结论:①;②;③;④(为任意实数);⑤方程有两个实数根,一个大于3,一个小于-1.其中结论正确的个数为( )
12. 如图是抛物线的部分图象,图象过点 , 对称轴为直线 , 有下列五个结论:①;②;③;④(为任意实数);⑤方程有两个实数根,一个大于3,一个小于-1.其中结论正确的个数为( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
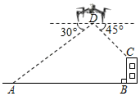
13. 如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面米的处,无人机测得操控者的俯角为30°,测得点处的俯角为45°.又经过人工测量操控者和教学楼之间的水平距离为80米,教学楼的高度米.(注:点、、、都在同一平面上,参考数据: , 结果保留整数).
 14. 已知二次函数的图象顶点坐标是 , 还经过点 , 它的图象与轴交于、两点,则线段的长为 .15. 有四张大小和背面完全相同的不透明卡片,正面分别印有等边三角形、平行四边形、菱形和圆,将这四张卡片背面朝上洗匀,从中随机抽取两张卡片,所抽取的卡片正面上的图形都既是轴对称图形,又是中心对称图形的概率是 .16. 如图,点、都在反比例函数的图象上,点是直线上的一个动点,则的最小值是 .
14. 已知二次函数的图象顶点坐标是 , 还经过点 , 它的图象与轴交于、两点,则线段的长为 .15. 有四张大小和背面完全相同的不透明卡片,正面分别印有等边三角形、平行四边形、菱形和圆,将这四张卡片背面朝上洗匀,从中随机抽取两张卡片,所抽取的卡片正面上的图形都既是轴对称图形,又是中心对称图形的概率是 .16. 如图,点、都在反比例函数的图象上,点是直线上的一个动点,则的最小值是 . 17. 如图,是的直径,弦 , 垂足为 , , , 则 .
17. 如图,是的直径,弦 , 垂足为 , , , 则 .
三、解答题
-
18. 计算: .19. 北京将于2022年举办冬奥会和冬残奥会,中国将成为一个举办过五次各类奥林匹克运动会的国家.小亮是个集邮爱好者,他收集了如图所示的三张纪念邮票(除正面内容不同外,其余均相同),现将三张邮票背面朝上,洗匀放好.
 (1)、小亮从中随机抽取一张邮票是“冬奥会会徽”的概率是;(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,请你用列表或画树状图的方法求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这三张邮票依次分别用字母A,B,C表示)20. 某校为检测师生体温,在学校门口安装了某型号的测温门,如图为该“测温门”截面示意图,身高1.7米的小聪做了如下实验:当他在地面处时“测温门”开始显示额头温度,此时在额头处测得的仰角为45°;当他在地面处时,“测温门”停止显示额头温度,此时在额头处测得的仰角为58°.如果测温门顶部处距地面的高度为3.3米,求小聪在有效测温区间的长度约为多少米?(结果保留一位小数,注:额头到地面的距离以身高计, , , . )
(1)、小亮从中随机抽取一张邮票是“冬奥会会徽”的概率是;(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,请你用列表或画树状图的方法求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这三张邮票依次分别用字母A,B,C表示)20. 某校为检测师生体温,在学校门口安装了某型号的测温门,如图为该“测温门”截面示意图,身高1.7米的小聪做了如下实验:当他在地面处时“测温门”开始显示额头温度,此时在额头处测得的仰角为45°;当他在地面处时,“测温门”停止显示额头温度,此时在额头处测得的仰角为58°.如果测温门顶部处距地面的高度为3.3米,求小聪在有效测温区间的长度约为多少米?(结果保留一位小数,注:额头到地面的距离以身高计, , , . ) 21. 如图,直线与双曲线交于、两点,直线与轴交于点 , 与轴交于点 , , , 点的纵坐标为-8.
21. 如图,直线与双曲线交于、两点,直线与轴交于点 , 与轴交于点 , , , 点的纵坐标为-8. (1)、求反比例函数的解析式;(2)、求的面积;(3)、直接写出不等式的解集.22. 2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量(件)与销售单价(元)之间的函数关系如图所示,设每月获得的利润为(元).
(1)、求反比例函数的解析式;(2)、求的面积;(3)、直接写出不等式的解集.22. 2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量(件)与销售单价(元)之间的函数关系如图所示,设每月获得的利润为(元).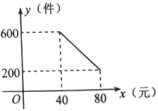 (1)、求出每月的销售量(件)与销售单价(元)之间的函数关系式;(2)、这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?(3)、为了扩大冬奥会的影响,物价部门规定这种文化衫的销售单价不高于60元,该商店销售这种文化衫每月要获得最大利润,销售单价应定为多少元?每月的最大利润为多少元?
(1)、求出每月的销售量(件)与销售单价(元)之间的函数关系式;(2)、这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?(3)、为了扩大冬奥会的影响,物价部门规定这种文化衫的销售单价不高于60元,该商店销售这种文化衫每月要获得最大利润,销售单价应定为多少元?每月的最大利润为多少元?

