山东省济南市槐荫区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 在下面的四个几何体中,主视图是三角形的是( )A、
 B、
B、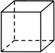 C、
C、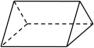 D、
D、 2. 已知 , 则的值为( )A、 B、 C、 D、3. 抛物线的对称轴为( )A、直线x=-1 B、直线x=-4 C、直线x=1 D、直线x=44. 如图,在 中, ,则AC的长为( )
2. 已知 , 则的值为( )A、 B、 C、 D、3. 抛物线的对称轴为( )A、直线x=-1 B、直线x=-4 C、直线x=1 D、直线x=44. 如图,在 中, ,则AC的长为( ) A、5 B、8 C、12 D、135. 如图,点A、B、C在⊙O上,∠CAB=70°,则∠BOC等于( )
A、5 B、8 C、12 D、135. 如图,点A、B、C在⊙O上,∠CAB=70°,则∠BOC等于( ) A、100° B、110° C、130° D、140°6. 若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为( )A、 B、 C、 D、7. 如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=35°,则∠AOB的度数为( )
A、100° B、110° C、130° D、140°6. 若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为( )A、 B、 C、 D、7. 如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=35°,则∠AOB的度数为( )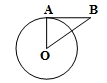 A、65° B、55° C、45° D、35°8. 已知点A(-2,y1),B(1,y2),C(3,y3)在二次函数图象上,则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、9. 如图,已知△ABC∽△ACP,∠A=70°,∠APC=65°,则∠B的度数为( )
A、65° B、55° C、45° D、35°8. 已知点A(-2,y1),B(1,y2),C(3,y3)在二次函数图象上,则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、9. 如图,已知△ABC∽△ACP,∠A=70°,∠APC=65°,则∠B的度数为( )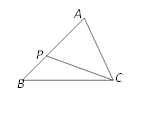 A、45° B、50° C、55° D、60°10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列选项不正确的是( )
A、45° B、50° C、55° D、60°10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列选项不正确的是( ) A、ac<0 B、对称轴为直线 C、a-b+c>0 D、11. 如图,正方形ABCD的相邻两个顶点C、D分别在x轴、y轴上,且满足BD∥x轴,反比例函数y=(x<0)的图象经过正方形的中心E,若正方形的面积为8,则该反比例函数的解析式为( )
A、ac<0 B、对称轴为直线 C、a-b+c>0 D、11. 如图,正方形ABCD的相邻两个顶点C、D分别在x轴、y轴上,且满足BD∥x轴,反比例函数y=(x<0)的图象经过正方形的中心E,若正方形的面积为8,则该反比例函数的解析式为( ) A、y= B、y=- C、y= D、y=-12. 如图,矩形ABCD中,AB=1,BC= , 点P为CD边上的一个动点,连接AP,将四边形ABCP沿AP折叠至四边形AB'C'P,在点P由点C运动到点D的过程中,点C'运动的路径长为( )
A、y= B、y=- C、y= D、y=-12. 如图,矩形ABCD中,AB=1,BC= , 点P为CD边上的一个动点,连接AP,将四边形ABCP沿AP折叠至四边形AB'C'P,在点P由点C运动到点D的过程中,点C'运动的路径长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
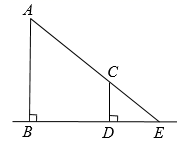
13. 若tanA= , 则∠A= .14. 学习投影后,小华利用灯光下自己的影子长度来测量一路灯的高度.如图,身高1.7m的小明从路灯灯泡A的正下方点B处,沿着平直的道路走8m到达点D处,测得影子DE长是2m,则路灯灯泡A离地面的高度AB为m.
 15. 在正方形网格中,的位置如图所示,则sin∠BAC的值为 .
15. 在正方形网格中,的位置如图所示,则sin∠BAC的值为 . 16. 已知扇形的圆心角为120°,半径为9,则该扇形的面积为 .17. 如图,在△ABC中,点D是边AB上的一点,∠ACD=∠B,AD=2,BD=6,则边AC的长为 .
16. 已知扇形的圆心角为120°,半径为9,则该扇形的面积为 .17. 如图,在△ABC中,点D是边AB上的一点,∠ACD=∠B,AD=2,BD=6,则边AC的长为 .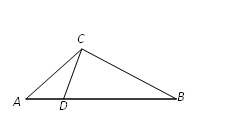 18. 如图,在扇形OAB中,∠AOB=105°,OA=4,将扇形OAB沿着过点B的直线折叠,点O恰好落在弧的点D处,折痕BC交OA于点C,则阴影部分的面积为 .
18. 如图,在扇形OAB中,∠AOB=105°,OA=4,将扇形OAB沿着过点B的直线折叠,点O恰好落在弧的点D处,折痕BC交OA于点C,则阴影部分的面积为 .
三、解答题
-
19. 计算6sin30°20. 如图,△ABC的三个顶点的坐标分别为A(3,1),B(1,2),C(4,3).
 (1)、以原点O为位似中心,在第一象限内将△ABC放大为原来的2倍得到△A1B1C1 , 作出△A1B1C1 , 写出A1 , B1 , C1的坐标;(2)、四边形AA1B1B的面积为 .21. 如图,在平行四边形ABCD中,E为AB边上一点,连接CE,F为CE上一点,且∠DFE=∠A.求证:△DCF∽△CEB.
(1)、以原点O为位似中心,在第一象限内将△ABC放大为原来的2倍得到△A1B1C1 , 作出△A1B1C1 , 写出A1 , B1 , C1的坐标;(2)、四边形AA1B1B的面积为 .21. 如图,在平行四边形ABCD中,E为AB边上一点,连接CE,F为CE上一点,且∠DFE=∠A.求证:△DCF∽△CEB. 22. 请阅读下列解题过程:
22. 请阅读下列解题过程:解一元二次不等式:x2-5x>0.
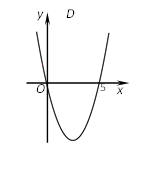
解:设x2-5x=0,解得:x1=0,x2=5,则抛物线y=x2-5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2-5x的大致图象(如图所示).由图象可知:当x<0或x>5时函数图象位于x轴上方,此时y>0,即x2-5x>0.
所以一元二次不等式x2-5x>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)、上述解题过程中,渗透了下列数学思想中的和 . (只填序号)①转化思想;②分类讨论思想;③数形结合思想.
(2)、用类似的方法解一元二次不等式:x2-2x-3<0.23. 如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50米至B处,测得仰角为60°. (1)、求证:AB=BD;(2)、求塔高CD.(小明的身高忽略不计,结果保留根号)24. 如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)、求证:AB=BD;(2)、求塔高CD.(小明的身高忽略不计,结果保留根号)24. 如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD. (1)、求证:△ABD≌△CDB;(2)、若∠DBE=37°,求∠ADC的度数.25. 在平面直角坐标系中,已知OA=10cm,OB=5cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤5),
(1)、求证:△ABD≌△CDB;(2)、若∠DBE=37°,求∠ADC的度数.25. 在平面直角坐标系中,已知OA=10cm,OB=5cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤5), (1)、用含t的代数式表示:线段PO=cm;OQ=cm.(2)、当t为何值时△POQ的面积为6cm2?(3)、当△POQ与△AOB相似时,求出t的值.26. 如图1,矩形OABC的顶点A、C分别落在x轴、y轴的正半轴上,点B(4,3),反比例函数y=(x>0)的图象与AB、BC分别交于D、E两点,BD=1,点P是线段OA上一动点.
(1)、用含t的代数式表示:线段PO=cm;OQ=cm.(2)、当t为何值时△POQ的面积为6cm2?(3)、当△POQ与△AOB相似时,求出t的值.26. 如图1,矩形OABC的顶点A、C分别落在x轴、y轴的正半轴上,点B(4,3),反比例函数y=(x>0)的图象与AB、BC分别交于D、E两点,BD=1,点P是线段OA上一动点.
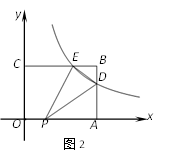
 (1)、求反比例函数关系式和点E的坐标;(2)、如图2,连接PE、PD,求PD+PE的最小值;(3)、如图3,当∠PDO=45°时,求线段OP的长.27. 二次函数y=ax2+bx+4(a≠0)的图象经过点A(-4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点,连接BP、AC,过点P作PD⊥x轴于点D.
(1)、求反比例函数关系式和点E的坐标;(2)、如图2,连接PE、PD,求PD+PE的最小值;(3)、如图3,当∠PDO=45°时,求线段OP的长.27. 二次函数y=ax2+bx+4(a≠0)的图象经过点A(-4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点,连接BP、AC,过点P作PD⊥x轴于点D. (1)、求二次函数的表达式;(2)、连接PA,PC,求的最大值;(3)、连接BC,当∠DPB=2∠BCO时,求直线BP的表达式.
(1)、求二次函数的表达式;(2)、连接PA,PC,求的最大值;(3)、连接BC,当∠DPB=2∠BCO时,求直线BP的表达式.