山东省滨州市无棣县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列说法正确的是（）

A、“明天有雪”是随机事件 B、“太阳从西方升起”是必然事件 C、“翻开九年上册数学课本，恰好是第88页”是不可能事件 D、射击运动员射击一次，命中十环是必然事件

查看试题解析
2. 已知反比例函数 $y = - \frac{2}{x}$ ，下列说法中不正确的是（）

A、图象经过点 $(1 ， - 2)$ B、图象位于第二、四象限 C、图象关于直线 $y = - x$ 对称 D、y随x的增大而增大

查看试题解析
3. 已知二次函数 $y = x^{2} - 2 x + m$ 的图像与x轴的一个交点为 $(- 1 ， 0)$ ，则它与x轴的另一个交点的坐标为（）

A、 $(- 3 ， 0)$ B、 $(3 ， 0)$ C、 $(1 ， 0)$ D、 $(- 2 ， 0)$

查看试题解析
4. 如图， $△ A B C$ 内接于 $⊙ O$ ， $C D$ 是 $⊙ O$ 的直径， $∠ B C D = 56 °$ ，则 $∠ A$ 的度数是（）

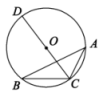A、36° B、34° C、56° D、78°

查看试题解析
5. 如图， $A D ∥ B E ∥ C F$ ，直线 $l_{1} ， l_{2}$ 与这三条平行线分别交于点A、B、C和点D、E、F，若 $A B = 9 ， B C = 6 ， E F = 4$ ，则DE的长度是（）

A、 $\frac{8}{3}$ B、 $\frac{27}{2}$ C、6 D、10

查看试题解析
6. 用一条长 $60 c m$ 的绳子围成一个面积为 $200 c m^{2}$ 的长方形．设长方形的长为 $x c m$ ，则可列方程为（）

A、 $x (30 - x) = 200$ B、 $x (30 + x) = 200$ C、 $x (60 + x) = 200$ D、 $x (60 - x) = 200$

查看试题解析
7. 如图，将正方形ABCD绕点A顺时针旋转 $38 °$ ，得到正方形 $A E F G$ ， DB的延长线交EF于点H，则 $∠ D H E$ 的大小为（）

A、76° B、97° C、90° D、114°

查看试题解析
8. 如图平行四边形ABCD中，F为BC中点，延长AD至E，使 $A D ： A E = 3 ： 4$ ，连结EF交DC于点G，则 $S_{△ D E G} ： S_{△ C F G} =$ （）

A、2∶3 B、4∶9 C、9∶4 D、3∶2

查看试题解析
9. 阅读理解：如图1，在平面内选一定点O，引一条有方向的射线 $O x$ ，再选定一个单位长度，那么平面上任一点M的位置可由 $∠ M O x$ 的度数 $θ$ 与 $O M$ 的长度m确定，有序数对 $(θ ， m)$ 称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．
应用：在图2的极坐标系下，如果正六边形的边长为4，有一边 $O A$ 在射线 $O x$ 上，则正六边形的顶点C的极坐标应记为（）

A、 $(60 ° ， 8)$ B、 $(45 ° ， 8)$ C、 $(60 ° ， 4 \sqrt{2})$ D、 $(45 ° ， 2 \sqrt{2})$

查看试题解析
10. 若抛物线y＝kx²﹣2x﹣1与x轴有两个不同的交点，则k的取值范围为（）

A、k＞﹣1 B、k≥﹣1 C、k＞﹣1且k≠0 D、k≥﹣1且k≠0

查看试题解析
11. 如图，直线 $y = \frac{1}{2} x - 1$ 与x轴交于点B，双曲线 $y = \frac{k}{x}$ （x＞0）交于点A，过点B作x轴的垂线，与双曲线 $y = \frac{k}{x}$ 交于点C，且AB=AC，则k的值为（）

A、2 B、3 C、4 D、6

查看试题解析
12. 已知抛物线 $y = a x^{2} + b x + c$ 上部分点的横坐标x与纵坐标y的对应值如下表：
x
…
-4
-3
-2
-1
0
…
y
…
-3
m
1
0
-3
…
有以下几个结论：①抛物线 $y = a x^{2} + b x + c$ 的开口向下；②抛物线 $y = a x^{2} + b x + c$ 的对称轴为直线 $x = - 2$ ；③关于x的方程 $a x^{2} + b x + c = 0$ 的根为-3和-1；④当 $y < 0$ 时，x的取值范围是 $- 3 < x < - 1$ ．其中正确的有（）个．

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

13. 方程x²＝x的解为．

查看试题解析
14. 如图，线段AB两个端点的坐标分别为 $A (12 ， 12) ， B (16 ， 4)$ ，以原点O为位似中心，在第一象限内将线段AB缩小为原来的 $\frac{1}{2}$ 后得到线段CD，则端点D的坐标为．

查看试题解析
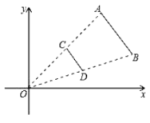15. 如图，在平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上， $∠ A O B = ∠ B = 30 ° ， O B = 4$ ．将 $△ A O B$ 绕点O逆时针旋转 $90 °$ ，点B的对应点 $B$ 的坐标是．

查看试题解析
16. 如图，AB是半圆O的直径，半圆的半径为4，点C，D在半圆上， $O C ⊥ A B ， \overset{⌢}{B D} = 2 \overset{⌢}{C D}$ ，点P是OC上的一个动点，则 $B P + D P$ 的最小值为．

查看试题解析
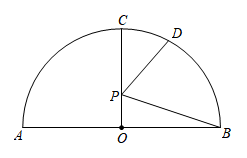17. 如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程，它是一条经过A、M、C三点的抛物线．其中A点离地面1.4米，M点是足球运动过程中的最高点，离地面3.2米，离守门员的水平距离为6米，点C是球落地时的第一点．那么足球第一次落地点C距守门员的水平距离为米．

查看试题解析

三、解答题

18. 在一次综合复习能力检测中，爱国同学的填空题的答卷情况如下，他的得分是分．

姓名：爱国得分：

填空题（每题2分，共10分）

①已知 $\frac{x}{y} = \frac{1}{3}$ ，则 $\frac{x + y}{y}$ 的值为（ $\frac{4}{3}$ ）．

②已知扇形的圆心角为60º，半径为1，则扇形的弧长为（ $\frac{π}{3}$ ）．

③两个相似三角形对应边上的高的比是2∶3，那么这两个三角形面积的比是（2∶3）．

④一元二次方程 $x^{2} + p x - 2 = 0$ 的一个根为2，则p的值为（-1）．

⑤在一个不透明的袋子里装有红球和白球共30个，这些球除颜色外其余都相同．小明通过多次试验发现，摸出白球的频率稳定在0.3左右，则袋子里可能有（9）个红球．

查看试题解析

19.

(1)、二次函数 $y = x^{2} + b x + c$ 的图象过点 $B (0 ， - 3)$ ，它与反比例函数 $y = - \frac{6}{x}$ 的图象交于点 $A (m ， 3)$ ，试求这个二次函数的解析式．

(2)、解方程： $3 x^{2} - 4 x - 1 = 0$ ．

查看试题解析
20.

(1)、如图 $⊙ O$ 为水管横截面，水面宽 $A B = 48 c m$ ，水的最大深度为 $36 c m$ ，求 $⊙ O$ 的半径．

(2)、如图，在等边三角形 $A B C$ 中，点E为 $C B$ 边上一点（与点C不重合），点F是 $A C$ 边上一点，若 $B C = 10 ， E C = 6 ， ∠ A E F = 60 °$ ，求 $A F$ 的长度．

查看试题解析
21. ETC（ Electronic Toll Collection ）不停车收费系统是目前世界上最先进的路桥收费方式.安装有ETC的车辆通过路桥收费站无需停车就能交纳费用.某高速路口收费站有A，B，C，D四个ETC通道，车辆可任意选择一个ETC通道通过，且通过每个ETC通道的可能性相同，一天，小李和小赵分别驾驶安装有ETC的汽车经过此收费站.

(1)、求小李通过A通道的概率；

(2)、请用列表或画树状图的方法表示出两人通过此收费站的所有可能结果，并求出小李和小赵经过相同通道的概率.

查看试题解析
22. 如图，在正方形ABCD中，点E是AB的中点，延长BC到点F，使CF=AE．

(1)、求证：DE=DF；

(2)、在（1）的条件下，把△ADE绕点D逆时针旋转多少度后与△CDF重合；

(3)、现把 $△ D C F$ 向左平移，使 $D C$ 与AB重合，得 $△ A B H$ ， AH交ED于点G．若 $A D = 8$ ，求 $E G$ 的长．

查看试题解析
23. 为了迎接2022年春节，我县古城风景区内开发了冰上滑雪运动项目，某体育用品商店抓住这一商机购进一批滑雪板，若每件进价为50元，售价为66元，每星期可卖出40件．为了鼓励大家多参加冰上滑雪运动，同时降低库存，商家决定降价促销，根据市场调查，每件降价1元，每星期可多卖出4件．

(1)、若设每件滑雪板降价x元，每星期的销售量为y件，写出y与x之间的函数关系式，（不用标出x的取值范围）；

(2)、降价后，商家要使每星期的利润最大，应将售价定为每件多少元？最大销售利润多少？

查看试题解析
24. 如图，AB是 $⊙ O$ 的直径，点F在 $⊙ O$ 上，AE平分 $∠ C A D$ 交 $⊙ O$ 于点E，过点E作 $E D ⊥ A F$ ，交AF的延长线于点D，延长DE、AB相交于点C．

(1)、求证：CD是 $⊙ O$ 的切线；

(2)、若 $A B = 10 ， \frac{E D}{A D} = \frac{1}{2}$ ，求BC的长．

查看试题解析
25. 在矩形 $A O B C$ 中，分别以 $O B ， O A$ 所在直线为x轴和y轴，建立如图所示的平面直角坐标系．A点坐标为 $(0 ， 3)$ ， B点坐标为 $(4 ， 0)$ ， F是 $B C$ 上的一个动点（不与B、C重合），过F点的反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与 $A C$ 边交于点E，连接 $O E ， O F$ ，作直线EF．

(1)、若 $C F = 2$ ，求反比例函数解新式；

(2)、在（1）的条件下求出 $△ E O F$ 的面积；

(3)、在点F的运动过程中，试说明 $\frac{E C}{F C}$ 是定值．

查看试题解析
26. 抛物线 $y = a x^{2} + b c + c$ 的对称轴为直线 $x = 1$ ，该抛物线与x轴的两个交点分别为A和B，与y轴的交点为C，其中 $A (- 1 ， 0) ， O C = 3$ ．

(1)、求出抛物线的解析式；

(2)、若抛物线上存在一点P，使得 $△ P O C$ 的面积是 $△ B O C$ 的面积的2倍，求点P的坐标；

(3)、点M是线段BC上一点，过点M作x轴的垂线交抛物线于点D，求线段MD长度的最大值．

查看试题解析

x	…	-4	-3	-2	-1	0	…
y	…	-3	m	1	0	-3	…