内蒙古鄂尔多斯市准格尔旗2021-2022学年九年级上学期期末考试数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 垃圾分类是资源，垃圾混置是垃圾．下列可回收物、有害垃圾、厨余垃圾、其他垃圾四种垃圾回收标识中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 将抛物线y＝2（x﹣3）²+1向左平移2个单位长度，再向下平移3个单位长度，则平移后抛物线的顶点坐标是（）

A、（5，4） B、（1，﹣2） C、（﹣1，﹣2） D、（﹣5，﹣2）

查看试题解析
3. 下列事件中，是必然事件的是（）

A、400人中有两个人的生日在同一天 B、两条线段可以组成一个三角形 C、早上的太阳从西方升起 D、打开电视机，它正在放动画片

查看试题解析
4. 如图，下列条件不能判定 $Δ A C D$ 与 $Δ A B C$ 相似的是（）

A、 $\frac{C D}{B C} = \frac{A C}{A B}$ B、 $\frac{A C}{A B} = \frac{A D}{A C}$ C、 $∠ A D C = ∠ A C B$ D、 $∠ A C D = ∠ B$

查看试题解析
5. 如图，已知CD为⊙O的直径，过点D的弦DE平行于半径OA，若弧CE的度数是92°，则∠C的度数是（）

A、46° B、88° C、24° D、23°

查看试题解析
6. 如图， $A B$ 是⊙O的弦，且 $A B = 6$ ，点 $C$ 是弧 $A B$ 中点，点 $D$ 是优弧 $A B$ 上的一点， $∠ A D C = 30 °$ ，则圆心 $O$ 到弦 $A B$ 的距离等于（）

A、 $2 \sqrt{3}$ B、 $\sqrt{3}$ C、 $\frac{3}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
7. 一个同学经过培训后会做某项实验，回到班级后第一节课他教会了若干个同学，第二节课会做的同学每人又教会了同样多的同学，这样全班共有36人会做这项实验，若设1人每次能教会x名同学，则可列方程为（）

A、x＋（x＋1）x＝36 B、（x＋1）²＝36 C、1＋x＋x²＝36 D、x＋（x＋1）²＝36

查看试题解析
8. ①三点确定一个圆；②平分弦的直径平分弦所对的弧；③同圆或等圆中，相等的弦所对的圆心角相等；④在半径为4的圆中，30°的圆心角所对的弧长为 $\frac{π}{3}$ ；从上述4个命题中任取一个，是真命题的概率是（）

A、1 B、 $\frac{3}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
9. 如图所示是抛物线y＝ax²+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①a﹣b+c＞0；②3a+c＞0；③b²＝4a（c﹣n）；④一元二次方程ax²+bx+c＝n+1没有实数根.其中正确的结论个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在平面直角坐标系中放置 $Rt △ A B C ， ∠ A B C = 90^{\circ}$ ，点 $A (3 ， 4)$ .现将 $△ A B C$ 沿 $x$ 轴的正方向无滑动翻转，依次得到 $△ A_{1} B_{1} C_{1} ， △ A_{2} B_{2} C_{2} ， △ A_{3} B_{3} C_{3} \dots$ 连续翻转 14 次，则经过 $△ A_{14} B_{14} C_{14}$ 三顶点的抛物线解析式为（）

A、 $y = - \frac{3}{5} (x - 51) (x - 55)$ B、 $y = - \frac{5}{12} (x - 51) (x - 55)$ C、 $y = - \frac{3}{5} (x - 55) (x - 60)$ D、 $y = - \frac{5}{12} (x - 55) (x - 60)$

查看试题解析

二、填空题

11. 在平面直角坐标系中，将点 $A (1 ， 3)$ 绕坐标原点顺时针旋转180°后得点B，则点B的坐标为．

查看试题解析
12. 已知圆锥的侧面展开图的面积是 $24 π$ ，圆心角是60°，则这个圆锥的底面圆的半径是．

查看试题解析
13. 已知m是一元二次方程 $x^{2} - x - 2021 = 0$ 的一个根，则代数式 $m^{2} - m =$ ．

查看试题解析
14. 如图，AB是半圆的直径，C、D是半圆上的两点，∠CAB＝24°，则∠ADC的度数为．

查看试题解析
15. 已知点D，E分别在△ABC的边AB，AC上，△ADE，△DEC，△BCD的面积之比为4：2：3，∠ACD=∠ADE，CD= $\sqrt{6}$ ，则BC的长为．

查看试题解析
16. 如图，已知正方形ABCD的边长为6，点E是AB边上一动点，连接ED，将ED绕点E顺时针旋转90°到EF，连接DF，CF，则DF+CF的最小值是．

查看试题解析

三、解答题

17. 已知关于x的方程 $(k - 1) x^{2} + 4 x + 1 = 0$ ．

(1)、当k时，方程 $(k - 1) x^{2} + 4 x + 1 = 0$ 是一元二次方程；

(2)、若方程有两个实数根，求k的取值范围；

查看试题解析
18. 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△OAB的三个顶点O（0，0）、A（4，1）、B（4，4）均在格点上．

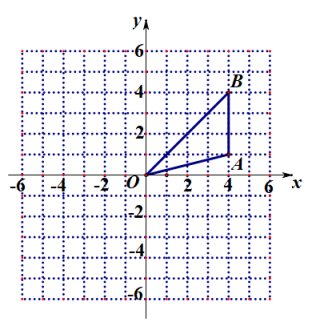(1)、画出△OAB绕原点 $O$ 顺时针旋转 $90 °$ 后得到的△ $O A_{1} B_{1}$ ，并写出点 $A_{1}$ 的坐标；

(2)、在（1）的条件下，求线段 $O A$ 在旋转过程中扫过的扇形的面积．

查看试题解析
19. 为了丰富校园文化生活，提高学生的综合素质，促进中学生全面发展，学校开展了多种社团活动.小明喜欢的社团有：合唱社团、足球社团、书法社团、科技社团（分别用字母A，B，C，D依次表示这四个社团），并把这四个字母分别写在四张完全相同的不透明的卡片的正面上，然后将这四张卡片背面朝上洗匀后放在桌面上.

(1)、小明从中随机抽取一张卡片是足球社团B的概率是.

(2)、小明先从中随机抽取一张卡片，记录下卡片上的字母后不放回，再从剩余的卡片中随机抽取一张卡片，记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.

查看试题解析
20. P为等边 $Δ A B C$ 内的一点，PA=10，PB=6，PC=8，将 $Δ A B P$ 绕点B顺时针旋转 $6 0^{∘}$ 到 $Δ C B P'$ 位置．

(1)、判断 $Δ B P P'$ 的形状，并说明理由；

(2)、求 $∠ B P C$ 的度数．

查看试题解析
21. 如图，AB是⊙O的直径，AC与⊙O交于点F，弦AD平分 $∠ B A C$ ， $D E ⊥ A C$ ，垂足为E.

(1)、试判断直线DE与⊙O的位置关系，并说明理由；

(2)、若⊙O的半径为2， $∠ B A C = 60^{°}$ ，求线段EF的长.

查看试题解析
22. 某商店经销一种学生用双肩包，已知这种双肩包的成本价为每个30元.市场调查发现，这种双肩包每天的销售量y（个）与销售单价x（元）有如下关系：y=﹣x+60（30≤x≤60）.设这种双肩包每天的销售利润为w元.

(1)、求w与x之间的函数关系式；

(2)、这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？

(3)、如果物价部门规定这种双肩包的销售单价不高于42元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少.

查看试题解析
23. 已知抛物线 $y = a x^{2} + b x + 3$ 经过点 $A (- 1 ， 0) 、 B (3 ， 0)$ ，与y轴交于点C，连接 $B C$ ．

(1)、求抛物线的解析式；

(2)、在直线 $B C$ 上方抛物线上取一点P，过点P作 $P Q ⊥ x$ 轴交 $B C$ 边于点Q，求 $P Q$ 的最大值；

(3)、在直线 $B C$ 上方抛物线上取一点D，连接 $O D ， C D$ ． $O D$ 交 $B C$ 于点F，当 $S_{△ C O F} ： S_{△ C D F} = 3 ： 2$ 时，求点D的坐标．

查看试题解析
24.

(1)、【问题背景】如图，在 $R t △ A B C$ 和 $R t △ A D E$ 中， $A B = A C ， A D = A E$ ，由已知可以得到：
① $△$ $≌ △$ ；

② $△$ $∽ △$ ．

(2)、【尝试应用】如图，在 $△ A B C$ 和 $△ A D E$ 中， $∠ A C B = ∠ A E D = 90 ° ， ∠ A B C = ∠ A D E = 30 °$ ，
求证： $△ A C E ∽ △ A B D$ ．

(3)、【问题解决】如图，在 $△ A B C$ 和 $△ A D E$ 中， $∠ B A C = ∠ D A E = 90 ° ， ∠ A B C = ∠ A D E = 30 ° ， A C$ 与 $D E$ 相交于点F，点D在 $B C$ 上， $\frac{A D}{B D} = \sqrt{3}$ ，求 $\frac{D F}{C F}$ 的值．

查看试题解析