广东省湛江市廉江市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列成语所描述的事件是必然事件的是（）

A、守株待兔 B、拔苗助长 C、瓮中捉鳖 D、水中捞月

查看试题解析
2. 用配方法解方程x²+2x-1=0时，配方结果正确的是（）

A、 ${(x + 1)}^{2} = 2$ B、 ${(x + 2)}^{2} = 2$ C、 ${(x + 1)}^{2} = 3$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
3. 下列二次函数中，其图象的对称轴为x＝﹣2的是（　　）

A、y＝2x²﹣2 B、y＝﹣2x²﹣2 C、y＝2 （x﹣2）² D、y＝（x+2）²

查看试题解析
4. 下列标志图中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 抛物线 $y = x^{2} - 2 x - 3$ 与 $x$ 轴的两个交点间的距离是（）

A、-1 B、-2 C、2 D、4

查看试题解析
6.
如图，PA、PB、分别切⊙O于A、B两点，∠P=40°，则∠C的度数为（　　）

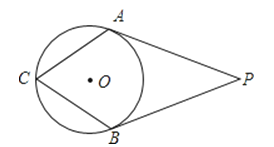A、40° B、140° C、70° D、80°

查看试题解析
7. 将抛物线y=2（x﹣4）²﹣1先向左平移4个单位长度，再向上平移2个单位长度，平移后所得抛物线的解析式为（）

A、y=2x²+1 B、y=2x²﹣3 C、y=2（x﹣8）²+1 D、y=2（x﹣8）²﹣3

查看试题解析
8. 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，若旋转角为20°，则∠1为（）

A、110° B、120° C、150° D、160°

查看试题解析
9. 如图，⊙O的半径为2，点C是圆上的一个动点，CA⊥x轴，CB⊥y轴，垂足分别为A、B，D是AB的中点，如果点C在圆上运动一周，那么点D运动过的路程长为（）

A、 $\frac{π}{4}$ B、 $\frac{π}{2}$ C、π D、2π

查看试题解析
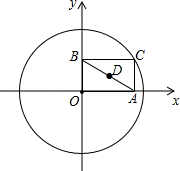10. 如图是二次函数y＝ax²+bx+c（a≠0）图象的一部分，对称轴是直线x＝﹣2．关于下列结论：①ab＜0；②b²﹣4ac＞0；③9a﹣3b+c＞0；④b﹣4a＝0；⑤方程ax²+bx＝0的两个根为x₁＝0，x₂＝﹣4，其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 一元二次方程 $(x - 3) (x - 2) = 0$ 的根是．

查看试题解析
12. 抛物线y＝（x+2）²+1的顶点坐标为．

查看试题解析
13. 从实数﹣1、﹣2、1中随机选取两个数，积为负数的概率是．

查看试题解析
14. 如图，△DEC与△ABC关于点C成中心对称，AB＝3，AC＝1，∠D＝90°，则AE的长是．

查看试题解析
15. 已知扇形的圆心角为120°，它所对弧长为20πcm，则扇形的半径为．

查看试题解析
16. 若关于x的函数 $y = {kx}^{2} + 2 x - 1$ 与x轴仅有一个公共点，则实数k的值为.

查看试题解析
17. 已知点P（x₀ ， m），Q（1，n）在二次函数y＝（x+a）（x﹣a﹣1）（a≠0）的图象上，且m＜n下列结论：①该二次函数与x轴交于点（﹣a，0）和（a+1，0）；②该二次函数的对称轴是x＝ $\frac{1}{2}$ ； ③该二次函数的最小值是（a+2）²； ④0＜x₀＜1．其中正确的是．（填写序号）

查看试题解析

三、解答题

18. 解方程： $x^{2} - 6 x + 8 = 0$

查看试题解析
19. 如图，AB是⊙O的直径，弦CD⊥AB于点E，OC＝10cm，CD＝16cm，求AE的长．

查看试题解析
20. 已知二次函数 $y = a x^{2} + b x$ 的图象过点 $(2 ， 0)$ ， $(- 1 ， 6)$ ．

(1)、求二次函数的关系式；

(2)、写出它与x轴的两个交点及顶点坐标．

查看试题解析
21. 益群精品店以每件21元的价格购进一批商品，该商品可以自行定价，若每件商品售价a元，则可卖出 $(350 - 10 a)$ 件，但物价局限定每件商品的利润不得超过20%，商店计划要盈利400元，需要进货多少件商品？每件应定价多少？

查看试题解析
22. 一个不透明的袋子中装有红、白两种颜色的小球，这些球除颜色外完全相同，其中红球有1个，若从中随机摸出一个球，这个球是白球的概率为 $\frac{2}{3}$ ．

(1)、请直接写出袋子中白球的个数．

(2)、随机摸出一个球后，放回并搅匀，再随机摸出一个球，求两次都摸到相同颜色的小球的概率．（请结合树状图或列表解答）

查看试题解析
23. ΔABC为等腰三角形，O为底边BC的中点，腰AB与 $⊙$ O相切于点D．
求证：AC是 $⊙$ O的切线．

查看试题解析
24. 已知关于x的一元二次方程x²﹣（2k+1）x+4k﹣3＝0，

(1)、求证：无论k取什么实数值，该方程总有两个不相等的实数根？

(2)、当Rt△ABC的斜边a＝ $\sqrt{31}$ ，且两条直角边的长b和c恰好是这个方程的两个根时，求k的值．

查看试题解析
25. 在平面直角坐标系中，已知抛物线y＝x²﹣2ax+4a+2（a是常数），

(1)、若该抛物线与x轴的一个交点为（﹣1，0），求a的值及该抛物线与x轴另一交点坐标；

(2)、不论a取何实数，该抛物线都经过定点H ．
①求点H的坐标；

②证明点H是所有抛物线顶点中纵坐标最大的点．

查看试题解析