广东省阳江市江城区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 25 = 0$ 的解为（）

A、 $x_{1} = x_{2} = 5$ B、 $x_{1} = 5$ ， $x_{2} = - 5$ C、 $x_{1} = x_{2} = - 5$ D、 $x_{1} = x_{2} = 25$

查看试题解析
2. 数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，是由两个正方体组成的几何体，则该几何体的左视图为（）

A、 B、 C、 D、

查看试题解析
4. 如图，AB是⊙O的直径，AC，BC是⊙O的弦，若 $∠ A = 20 °$ ，则 $∠ B$ 的度数为（）

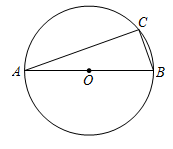A、70° B、90° C、40° D、60°

查看试题解析
5. 在Rt△ABC中，∠C＝90°，若AC＝6，BC＝8，则cosA的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
6. 若将抛物线y＝2x²﹣1向上平移2个单位，则所得抛物线对应的函数关系式为（）

A、y＝2(x﹣2)²﹣1 B、y＝2(x+2)²﹣1 C、y＝2x²﹣3 D、y＝2x²+1

查看试题解析
7. 如图， $△ A B C$ 与 $△ D E F$ 位似，点 $O$ 是它们的位似中心，其中 $O E = 3 O B$ ，则 $△ A B C$ 与 $△ D E F$ 的面积之比是（）

A、 $1 ： 2$ B、 $1 ： 4$ C、 $1 ： 3$ D、1：9

查看试题解析
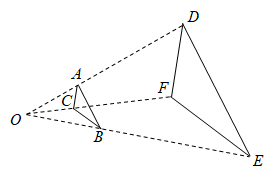8. 杨倩在东京奥运女子10米气步枪决赛中夺得冠军，为中国代表团揽入首枚金牌，随后杨倩同款“小黄鸭”发卡在电商平台上爆单，该款发卡在某电商平台上7月24日的销量为5000个，7月25日和7月26日的总销量是30000个．若7月25日和26日较前一天的增长率均为 $x$ ．则可列方程正确的是（）

A、 $5000 {(1 + x)}^{2} = 30000$ B、 $5000 (1 - x^{2}) = 30000$ C、 $5000 + 5000 (1 + x) + 5000 {(1 + x)}^{2} = 30000$ D、 $5000 (1 + x) + 5000 {(1 + x)}^{2} = 30000$

查看试题解析
9. 如图所示，在平面直角坐标系Oxy中，四边形OABC为矩形，点A、C分别在x轴、y轴上，点B在函数 $y_{1} = \frac{4}{x} (x > 0)$ 的图象上，边AB与函数 $y_{2} = \frac{2}{x} (x > 0)$ 的图象交于点D，则阴影部分ODBC的面积为（）

A、2 B、3 C、4 D、5

查看试题解析
10. 若 $a b < 0$ ，则反比例函数 $y = \frac{a b}{x}$ 与一次函数 $y = a x + b$ 在同一坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 在平面直角坐标系中点M（2，﹣4）关于原点对称的点的坐标为．

查看试题解析
12. 二次函数y=x²+1的图象的顶点坐标是．

查看试题解析
13. 中心角为30°的正多边形边数为．

查看试题解析
14. 国庆期间，小明从《长津湖》、《我和我的父辈》、《皮皮鲁与鲁西西》三部电影中随机选择一部观看，则选择《长津湖》观看的概率为；

查看试题解析
15.
如图，在8×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为．

查看试题解析
16. 如图，CD是⊙O的直径，AB是弦，CD⊥AB，若OB＝5，AB＝8，则AC的长为．

查看试题解析
17. 如图，将半径为2，圆心角为90°的扇形BAC绕点A逆时针旋转，在旋转过程中，点B落在扇形BAC的弧上的点B' 处，点C的对应点为点C' ，则阴影部分的面积为.

查看试题解析

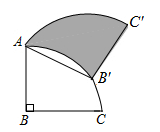
三、解答题

18. 解方程： $x^{2} - 6 x - 16 = 0$

查看试题解析
19. 已知关于x的方程x²﹣3x﹣m+3＝0总有两个不相等的实数根．

(1)、求m的取值范围；

(2)、若它的一个实数根是2，求m的值．

查看试题解析
20. 如图，正比例函数 $y = 2 x$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象有一个交点为 $P (2 ， m)$ .

(1)、求反比例函数 $y = \frac{k}{x}$ 函数表达式；

(2)、根据图象，直接写出当 $- 4 < x < - 1$ 时， $y$ 的取值范围.

查看试题解析
21. 为庆祝中国共产党建党100周年，某校组织全体学生进行了党史知识学习，并举行了党史知识竞赛，参赛学生均获奖．为了解本次竞赛获奖的分布情况，从中随机抽取了部分学生的获奖结果进行统计分析，学生的得分为整数，依据得分情况将获奖结果分为四个等级：A级为特等奖，B级（81—90分）为一等奖，C级（71—80分）为二等奖，D级（70分及以下）为三等奖，将统计结果绘制成了如图所示的两幅不完整的统计图，根据统计图中的信息解答下列问题：

(1)、本次被抽取的部分学生人数是 ▲ 人；并把条形统计图补充完整；

(2)、九年级一班有4名获特等奖的学生小明、小亮、小聪、小军，班主任要从中随机选择两名同学进行经验分享，利用列表法或画树状图，求小军被选中的概率．

查看试题解析
22. 钓鱼岛是我国固有领土，2021年4月26日，中华人民共和国自然资源部在其官网上公布《钓鱼岛及其附属岛屿地形地貌调查报告》，报告公布了钓鱼岛及其附属岛屿的高分辨率海岛地形数据．如图，点A是岛上最西端“西钓鱼”，点B是岛上最东端“东钓角”， $A B$ 长约3641米，点D是岛上的有小黄鱼岛，且 $A ， B ， D$ 三点共线．某日中国海监一艘执法船巡航到点C处时，恰好看到正北方的小黄鱼岛D，并测得 $∠ A C D = 70 °$ ， $∠ B C D = 45 °$ ．根据以上数据，请求出此时执法船距离小黄鱼岛D的距离 $C D$ （参考数据： $t a n 70 ° \approx 2.75$ ， $s i n 70 ° \approx 0.94$ ， $c o s 70 ° \approx 0.34$ ，结果精确到1米）．

查看试题解析
23. 在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕点B逆时针旋转一个角度α后得到△DBE，点A，C的对应点分别为点D，E．

(1)、如图1，若点D恰好落在边BC的延长线上，连接CE，求∠DEC的度数．

(2)、如图2，若α＝60°，F为BD的中点，连接CD，CF，EF，请判断四边形CDEF是什么特殊的四边形，并说明理由．

查看试题解析
24. 如图，在半径为4的⊙O中，E为 $\overset{⌢}{B C}$ 的中点，OE交BC于F，D为⊙O上一点，DE交AC于G，AD＝AG．

(1)、求证：AD是⊙O的切线；

(2)、若∠A＝60°，求ED的长．

查看试题解析
25. 已知抛物线y＝x²﹣2x﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点D是y轴右侧抛物线上一个动点．

(1)、求出点A，B，C的坐标；

(2)、如图1，当点D在第四象限时，求出△BCD面积的最大值，并求出这时点D坐标；

(3)、当∠DAB＝∠ABC时，求出点D的坐标．

查看试题解析