广东省梅州市兴宁市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，最小的数是（）

A、﹣2 B、 $- \sqrt{19}$ C、|﹣5| D、π

查看试题解析
2. 在以下四个标志中，既是轴对称图形又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 麒麟9000芯片是全球首款5nm 5G芯片，由我国的华为公司于2020年10月22日20：00发布，该芯片集成了多达153亿个晶体管．将153亿用科学记数法表示为（）

A、1.53×10² B、153× $1 0^{8}$ C、1.53× $1 0^{10}$ D、1.53× $1 0^{11}$

查看试题解析
4. 如图是一个几何体的三视图，则这个几何体是（）．

A、三棱锥 B、圆锥 C、三棱柱 D、圆柱

查看试题解析
5. 若正方形ABCD各边的中点依次为E、F、G、H，则四边形EFGH是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
6. 在同一平面直角坐标系中，一次函数 $y = k x + k (k \neq 0)$ 与反比例函数 $y = \frac{- k}{x} (k \neq 0)$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
7. 若点C为线段AB的黄金分割点，AB=8，则AC的长是（）

A、 $4 \sqrt{5}$ －4 B、9－ $3 \sqrt{5}$ C、 $3 \sqrt{5}$ －3或9－ $3 \sqrt{5}$ D、 $4 \sqrt{5}$ －4或12－ $4 \sqrt{5}$

查看试题解析
8. 在一个不透明的盒子中装有30个白、黄两种颜色的乒乓球，这些乒乓球除颜色外都相同．班长进行了多次的摸球试验，发现摸到黄色乒乓球的频率稳定在0.3左右，则盒子中的白色乒乓球的个数可能是（）

A、21个 B、15个 C、12个 D、9个

查看试题解析
9. 二次函数y＝﹣x²－3x＋1的图象的顶点在（）

A、第四象限 B、第三象限 C、第二象限 D、第一象限

查看试题解析
10. 二次函数y= $\frac{2}{3}$ x²的图象如图所示，点A₀位于坐标原点，A₁ ， A₂ ， A₃ ， …，A₂₀₂₃在y轴的正半轴上，B₁ ， B₂ ， B₃ ， …，B₂₀₂₃在二次函数y= $\frac{2}{3}$ x²第一象限的图象上，若△A₀B₁A₁ ， △A₁B₂A₂ ， △A₂B₃A₃ ， …，△A₂₀₂₂B₂₀₂₃A₂₀₂₃都是等边三角形，则△A₂₀₂₂B₂₀₂₃A₂₀₂₃的周长是（）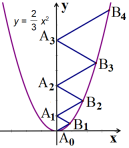

A、6069 B、6066 C、6063 D、6060

查看试题解析

二、填空题

11. 若 $2 x = 5 y$ ，则 $\frac{x + y}{x - y}$ 的值是．

查看试题解析
12. 若矩形ABCD的周长为26cm，对角线的长是 $\sqrt{129}$ cm，则它的面积是．

查看试题解析
13. 如图，已知点D、E分别是△ABC的边AC、BC上的动点，请你在不增加任何辅助图形与字母的情况下，补充一个条件，使图中的两个三角形是以点C为位似中心的位似图形，则可以补充的条件是．

查看试题解析
14. 若m、n是方程x²－3x－1=0的解，则m²－4m－n的值是．

查看试题解析
15. 小亮的身高1.8m，他在阳光下的影长为0.6m；同一时刻，学校的旗杆影长为3m，则该旗杆的高度是．

查看试题解析
16. 对称轴为直线x=1的抛物线y=ax²＋bx＋c（a、b、c为常数，且a≠0）如图所示，以下结论：①abc＜0，②b²＞4ac，③4a＋2b＋c＞0，④3a＋c＞0，⑤a＋b≤m（am＋b）（m为任意实数），⑥当x＜﹣1时，y随x的增大而减小．其中结论正确的是．（填写正确的结论的序号）

查看试题解析
17. 如图，四边形ABCD中，AB ∥CD，AD=4，AB=BC=BD=6，则∠ACD的正弦值是．

查看试题解析

三、解答题

18. 计算： ${(- \frac{1}{3})}^{- 3} + 8 \times s i n 45 ° \times c o s 30 ° - \sqrt{54}$

查看试题解析
19. 如图，某数学兴趣小组为测量一座古塔的高度，在古塔左侧的A点处测得古塔顶端D的仰角为30°，然后向古塔底端C前进30米到达点B处，测得古塔顶端D的仰角为45°，且点A、B、C在同一水平直线上，求古塔CD的高度．

查看试题解析
20. 某市准备举行初中生“党史知识竞赛”，学校通过初赛选出了2位男生A、B和2位女生C、D共4位选手，准备从4人中任选2人代表学校参加比赛．求所选代表都是女生的概率．

查看试题解析
21. 已知平行四边形ABCD，AC是它的对角线．

(1)、用尺规作AC的垂直平分线EF，垂足为O，EF交AB于点E，交CD于点F（不写作法，但要保留痕迹）；

(2)、连接AF、CE，求证：四边形AFCE是菱形；

查看试题解析
22. 某服装厂2021年10月份的生产成本是500万元，由于改进技术，生产成本逐月下降，12月份的生产成本是405万元．假设该厂从2021年11月起连续4个月的生产成本的下降率都是相同的．

(1)、求每个月生产成本的下降率；

(2)、该服装厂的厂长希望2022年1月份的生产成本能低于365万元，请你通过计算说明该厂长的目标能否实现．

查看试题解析
23. 如图，线段 CD∥AB，AD与BC交于点E．

(1)、求证； $A E \cdot C E = D E \cdot B E$ ；

(2)、过点E作EF∥AB，交AC于点F，如果AB=5，EF=2，求CD的长．

查看试题解析
24. 已知反比例函数y= $\frac{k}{x}$ 的图象经过点A（6，1）．

(1)、求该反比例函数的表达式；

(2)、如图，在反比例函数y= $\frac{k}{x}$ 在第一象限的图象上点A的左侧取点C，过点A作x轴的垂线交x轴于点H，过点C作y轴的垂线CE，垂足为点E，交直线AH于点D．
①过点A、点C分别作y轴、x轴的垂线，两条垂线相交于点B，求证：O、B、D三点共线；
②若AC=2CO，求证：∠OCE=3∠CDO．

查看试题解析
25. 如图，抛物线y＝ax²+bx－3与x轴交于A（﹣1，0），B（3，0）两点，过点A的直线l交抛物线于点C（2，n）．

(1)、求抛物线的解析式．

(2)、点P是线段AC上一个动点，过点P作x轴的垂线交抛物线于点E，求线段PE最大时点P的坐标．

(3)、点F是抛物线上的动点，在x轴上是否存在点D，使得以点A，C，D，F为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的点D的坐标；如果不存在，请说明理由．

查看试题解析