广东省揭阳市普宁市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
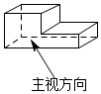
1. 下图所示的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,已知直线AB∥CD∥EF , BD=2,DF=4,则 的值为( )
2. 如图,已知直线AB∥CD∥EF , BD=2,DF=4,则 的值为( ) A、 B、 C、 D、13. 已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是( )A、sinA= B、tanA= C、tanB= D、cosB=4. 将二次函数 的图象向左平移1个单位长度,再向上平移2个单位后,所得图象的函数解析式是( )A、 B、 C、 D、5. 对于一元二次方程来说,当时,方程有两个相等的实数根,若将c的值在的基础上减小,则此时方程根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、不能确定;6. 如图,线段AB∥CD,连接AD,BC交于点O,若CD=2AB,则下列选项中不正确的是( )
A、 B、 C、 D、13. 已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是( )A、sinA= B、tanA= C、tanB= D、cosB=4. 将二次函数 的图象向左平移1个单位长度,再向上平移2个单位后,所得图象的函数解析式是( )A、 B、 C、 D、5. 对于一元二次方程来说,当时,方程有两个相等的实数根,若将c的值在的基础上减小,则此时方程根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、不能确定;6. 如图,线段AB∥CD,连接AD,BC交于点O,若CD=2AB,则下列选项中不正确的是( ) A、△AOB∽△DOC B、 C、 D、7. 下列说法中正确的是( )A、矩形的对角线平分每组对角; B、菱形的对角线相等且互相垂直; C、有一组邻边相等的矩形是正方形; D、对角线互相垂直的四边形是菱形.8. 某口袋里现有12个红球和若干个绿球(两种球除颜色外,其余完全相同),某同学随机的从该口袋里摸出一球,记下颜色后放回,共试验600次,其中有300次是红球,估计绿球个数为( )A、8 B、10 C、12 D、149. 如图,小明在学校操场A处测得旗杆的仰角为30°,沿AC方向行进10米至B处,测得仰角为45°,则旗杆的高度DC是( )
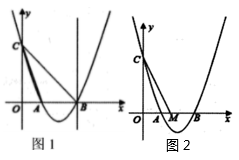
A、△AOB∽△DOC B、 C、 D、7. 下列说法中正确的是( )A、矩形的对角线平分每组对角; B、菱形的对角线相等且互相垂直; C、有一组邻边相等的矩形是正方形; D、对角线互相垂直的四边形是菱形.8. 某口袋里现有12个红球和若干个绿球(两种球除颜色外,其余完全相同),某同学随机的从该口袋里摸出一球,记下颜色后放回,共试验600次,其中有300次是红球,估计绿球个数为( )A、8 B、10 C、12 D、149. 如图,小明在学校操场A处测得旗杆的仰角为30°,沿AC方向行进10米至B处,测得仰角为45°,则旗杆的高度DC是( )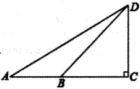 A、米 B、米 C、10米 D、米10. 一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( )
A、米 B、米 C、10米 D、米10. 一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( )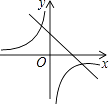 A、
A、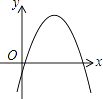 B、
B、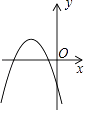 C、
C、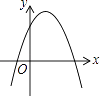 D、
D、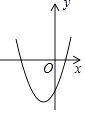
二、填空题
-
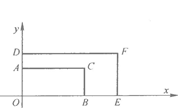
11. 计算: .12. 若(x,y,z均不为0),则 .13. 如图所示,矩形AOBC与DOEF是位似图形,且O为位似中心,相似比为1∶ , 若A(0,1)、B(2,0),则F点的坐标为.
 14. 如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.1m,则建筑物AB的高度约为 . (结果精确到0.1m,参考数据: , , )
14. 如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.1m,则建筑物AB的高度约为 . (结果精确到0.1m,参考数据: , , ) 15. 如图,正比例函数 与反比例函数 的图象相交于 , 两点,其中点 的横坐标为1.当 时, 的取值范围是 .
15. 如图,正比例函数 与反比例函数 的图象相交于 , 两点,其中点 的横坐标为1.当 时, 的取值范围是 .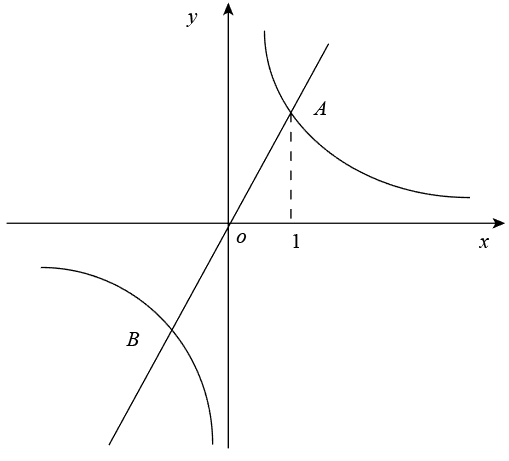 16. 用长12m的铝合金条制成矩形窗框(如图所示),那么这个窗户的最大透光面积是(中间横框所占的面积忽略不计)
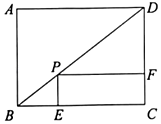
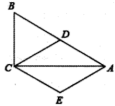
16. 用长12m的铝合金条制成矩形窗框(如图所示),那么这个窗户的最大透光面积是(中间横框所占的面积忽略不计) 17. 如图,在矩形ABCD中,E是AD边的中点,于点F,连接DF,下列四个结论:①△AEF∽△CAB;②;③;④ , 其中正确的结论是 . (填写序号即可)
17. 如图,在矩形ABCD中,E是AD边的中点,于点F,连接DF,下列四个结论:①△AEF∽△CAB;②;③;④ , 其中正确的结论是 . (填写序号即可)
三、解答题
-
18. 解方程:19. 江西两所医院分别有一男一女共4名医护人员支援湖北随州抗击疫情.(1)、若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 .(2)、若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.20. 已知二次函数 ,(1)、将二次函数的解析式化为 的形式;(2)、写出二次函数图象的开口方向、对称轴、顶点坐标.21. 如图,在Rt△ABC中, , D为AB的中点, , .
 (1)、证明:四边形ADCE为菱形;(2)、若 , , 求四边形ADCE的周长.22. 物美商场于今年年初以每件25元的进价购进一批商品.当商品售价为40元时,一月份销售256件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到400件.设二、三这两个月月平均增长率不变.(1)、求二、三这两个月的月平均增长率;(2)、从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?23. 如图,一次函数(k为常数,)与反比例函数(m为常数,)的图象交于点和 , 与y轴交于点M.
(1)、证明:四边形ADCE为菱形;(2)、若 , , 求四边形ADCE的周长.22. 物美商场于今年年初以每件25元的进价购进一批商品.当商品售价为40元时,一月份销售256件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到400件.设二、三这两个月月平均增长率不变.(1)、求二、三这两个月的月平均增长率;(2)、从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?23. 如图,一次函数(k为常数,)与反比例函数(m为常数,)的图象交于点和 , 与y轴交于点M. (1)、求一次函数与反比例函数的表达式;(2)、连接OA、OB,求△AOB的面积,
(1)、求一次函数与反比例函数的表达式;(2)、连接OA、OB,求△AOB的面积,