广东省揭阳市揭西县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列关系式中y是x的反比例函数的是（）

A、 $y = 5 x$ B、 $y = \frac{k}{x}$ C、 $y = \frac{5}{x^{2}}$ D、 $x y = 3$

查看试题解析
2. 如图，三视图正确的是（）

A、主视图 B、左视图 C、左视图 D、俯视图

查看试题解析
3. 用配方法解方程 $x^{2} - 2 x - 5 = 0$ 时，原方程应变形为（）

A、 ${(x + 1)}^{2} = 6$ B、 ${(x - 1)}^{2} = 6$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
4. 反比例函数 $y = \frac{k}{x}$ 的图象如图所示，则 $k$ 值可能是（）

A、－2 B、2 C、4 D、8

查看试题解析
5. 中国福利彩票“双色球”投注方法是每注选择6个红色球号码（从1－33的33个数中选择）加一个蓝色球号码（从1－16中16个数中选择），若最近三期蓝色号码球的开奖结果都为奇数，则下一期蓝色球的开奖结果（）

A、还是奇数 B、一定是偶数 C、是偶数的概率大于是奇数的概率 D、是偶数的概率为 $\frac{1}{2}$

查看试题解析
6. 已知四边形ABCD是平行四边形，下列结论：①当AB＝BC时，它是菱形；②当AC⊥BD时，它是菱形；③当∠ABC＝90°时，它是矩形；④当AC＝BD时，它是正方形，其中不正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，在△ABC中，点D、E在边AB上，点F、G在边AC上，且DF∥EG∥BC，AD＝DE＝EB，若 $S_{Δ A D F} = 1$ ，则 $S_{四边形 E B C G} =$ （）

A、3 B、4 C、5 D、6

查看试题解析
8. 若关于x的方程 ${(^{} + 2 x)}^{2} + 2 (x^{2} + 2 x) - 8 = 0$ 有实数根，则 $x^{2} + 2 x$ 的值为（）

A、－4 B、2 C、－4或2 D、4或－2

查看试题解析
9. 如图，△ABC的中线AD、BE相交于点F，过点E作EG∥AD交BC于点G，则EG∶AF的值是（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
10. 如图，正方形ABCD中，点E是边CD上的动点（不与点C、D重合），以CE为边向右作正方形CEFG，连接AF，点H是AF的中点，连接DH、CH．下列结论：①△ADH≌△CDH；②AF平分∠DFE；③若BC＝4，CG＝3，则AF＝5；④若 $\frac{C G}{B C} = \frac{1}{2}$ ，则 $\frac{S_{Δ E F I}}{S_{Δ D F I}} = \frac{1}{4}$ ．其中正确的有（）

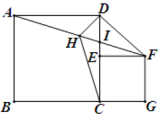A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 反比例函数 $y = \frac{k}{x}$ 图象上有两点A（－3，4）、B（m，2），则m＝．

查看试题解析
12. 为了估计池塘里有多少条鱼，从池塘里捕捞了1000条鱼做上标记，然后放回池塘里，经过一段时间，等有标记的鱼完全混合于鱼群中以后，再捕捞200条，若其中有标记的鱼有10条，则估计池塘里有鱼条．

查看试题解析
13. 已知一元二次方程（m－2） $x^{| m |}$ ＋3x－4＝0，那么m的值是．

查看试题解析
14. 在平面直角坐标系中，△ABC中点A的坐标是（2，3），以原点O为位似中心把△ABC放大，使放大后的三角形与△ABC的相似比为3：1，则点A的对应点A′的坐标为．

查看试题解析
15. 若一元二次方程 $x^{2} + \sqrt{3} x - 2 = 0$ 的两根分别为m与n，则 $\frac{m}{n} + \frac{n}{m} =$ ．

查看试题解析
16. 在矩形ABCD中，AB＝6，BC＝8，BD⊥DE交AC的延长线于点E，则DE＝．

查看试题解析
17. 如图，点A₁、A₂、A₃…An在x轴正半轴上，点B₁、B₂、B₃…Bn在反比例函数 $y = \frac{k}{x}$ （k＞0，x＞0）图象上，OA₁＝A₁A₂＝A₂A₃＝…＝An_－₁An，记矩形OA₁B₁C₁面积为S₁、矩形A₁A₂B₂C₂面积为S₂、矩形A₂A₃B₃C₃面积为S₃……，则S₂₀₂₁＝（用含k的代数式表示）．

查看试题解析

三、解答题

18. 我国新冠灭活疫苗主要来自三家生物制品公司，分别是A：科兴中维、B：北京所、C：武汉所．灭活疫苗一般需要接种2针，假如一人两次接种的疫苗的生产公司随机，请你用列表或树状图的方法求出一个人两次接种的疫苗刚好是同一家公司生产的概率．

查看试题解析
19. 如图，在△ABC中，AD平分∠BAC交BC于点D，DE∥AC交AB于点E，求证： $\frac{B D}{D C} = \frac{B E}{E D}$ ．

查看试题解析
20. 碧桂园进驻揭西，一栋栋高楼拔地而起．如图，小明（线段AB）利用学到的知识，计算楼房（线段CD）的层数，他把一镜子放在E处（点B、E、D共线），此时小明通过镜子刚好可以看到大楼的顶端C，若小明身高1.5m，测得BE＝1m，ED＝58m，碧桂园层高为2.9m，求这栋楼房有多少层？

查看试题解析
21. 近日在南非发现了新冠新型变异毒株奥密克戎，并且在广州也发现了此病毒病例，防止病毒的传播，外出戴口罩简单易行．某口罩生产商接到口罩订单，要求第一个月出货量为500万只，此后的每月出货量逐渐增长，并且前三个月总出货量为1820万只，则口罩生产商生产口罩的月平均增长率是多少？

查看试题解析
22. 如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BC相交于点N，连接BM，DN．

(1)、求证：四边形BMDN是菱形；

(2)、若AB＝4，AD＝8，求菱形BMDN的面积．

查看试题解析
23. 等腰三角形的三边长分别为 $a$ 、 $b$ 、 $c$ ，若 $a = 6$ ， $b$ 与 $c$ 是方程 $x^{2} - (3 m + 1) x + 2 m^{2} + 2 m = 0$ 的两根，求此三角形的周长．

查看试题解析
24. 如图，一次函数 $y = k x + 2$ 与 $y$ 轴交于点A，与反比例函数 $y = \frac{m}{x}$ 的图象相交于B、C两点，BD⊥ $y$ 轴交 $y$ 轴于点D，OA＝OD， $S_{Δ A B D} = 8$ ．

(1)、求一次函数与反比例函数的表达式；

(2)、求点C的坐标，并直接写出不等式 $k x + 2 > \frac{m}{x}$ 的解集；

(3)、在所在平面内，存在点E使以点B、C、D、E为顶点的四边形为平行四边形，请直接写出所有满足条件的点E的坐标．

查看试题解析
25. 如图1，在△ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm．如果点P由点B出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们的速度均为1cm/s．连接PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：

(1)、填空：用含t的代数式表示AQ＝， AP＝．

(2)、如图2，连接PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；

(3)、当t为何值时，△APQ是等腰三角形？

查看试题解析