广东省江门市蓬江区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，我国传统文化中的“福禄寿喜”图由四个图案构成，这四个图案中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中，属于随机事件的是（）

A、两条直线被第三条直线所截，同位角相等 B、圆是中心对称图形 C、早上太阳从西方升起 D、任意一个四边形的外角和等于360°

查看试题解析
3. 在一个不透明的盒子里，装有若干个除颜色不同外其余都相同的小球，如果盒子中装有4个红球且从中随机摸出一个球是红球的概率为 $\frac{1}{3}$ ，则盒子中小球个数为（）

A、15 B、12 C、10 D、8

查看试题解析
4. 若反比例函数y $= \frac{k + 1}{x}$ 的图象经过第二、四象限，则k的取值范围是（）

A、k＞1 B、k＜1 C、k＞﹣1 D、k＜﹣1

查看试题解析
5. 已知⊙O的直径为4，若 $O P = 4$ ，则点 $P$ 与⊙O的位置关系是（）

A、点 $P$ 在⊙O上 B、点 $P$ 在⊙O内 C、点 $P$ 在⊙O外 D、无法判断

查看试题解析
6. 关于抛物线y＝3x² ，下列说法正确的是（）

A、开口向下 B、顶点坐标为（0，3） C、对称轴为y轴 D、当x＜0时，函数y随x的增大而增大

查看试题解析
7. 关于x的方程x²﹣6x+k＝0的一个根是2，则k的值是（）

A、2 B、4 C、6 D、8

查看试题解析
8. 关于x的一元二次方程mx²+（2m﹣4）x+（m﹣2）＝0有两个实数根，则m的取值范围（）

A、m≥2 B、m≤2 C、m≥2且m≠0 D、m≤2且m≠0

查看试题解析
9. 如图，△ABC的外接圆半径为8，∠ACB＝60°，则AB的长为（）

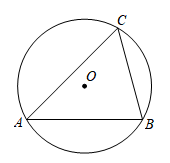A、8 $\sqrt{3}$ B、4 $\sqrt{3}$ C、6 D、4

查看试题解析
10. 某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是157，每个支干长出的小分支数目为（）

A、12 B、11 C、8 D、7

查看试题解析
11. 在平面直角坐标系中，点P是y轴正半轴上的任意一点，过点P作x轴的平行线，分别与反比例函数y $= - \frac{12}{x}$ 和y $= \frac{16}{x}$ 的图象交于点A和点B，若点C是x轴上任意一点，连接AC、BC，则△ABC的面积为（）

A、10 B、12 C、14 D、28

查看试题解析
12. 如图，将函数y $= - \frac{1}{2}$ （x+4）²+5的图象沿y轴向下平移得到一条新函数的图象，其中点A（﹣6，m），B（﹣1，n）平移后的对应点分别为点A'、B'，若曲线AB扫过的面积为30（图中的阴影部分），则新图象的函数表达式是（）

A、y $= - \frac{1}{2}$ （x+4）²﹣2 B、y $= - \frac{1}{2}$ （x+4）²﹣1 C、y $= - \frac{1}{2}$ （x+4）²+2 D、y $= - \frac{1}{2}$ （x+4）²+1

查看试题解析

二、填空题

13. 在平面直角坐标系中，点 $P (3 ， - 2)$ 关于原点对称的点的坐标是.

查看试题解析
14. 一元二次方程2x（x﹣1）﹣3＝0的一次项系数为．

查看试题解析
15. 已知二次函数y＝﹣x²﹣2x+m的部分图象如图所示，则关于x的一元二次方程﹣x²﹣2x+m＝0的解为．

查看试题解析
16. 一个扇形的弧长是10πcm，面积是75πcm² ，则扇形的圆心角是．

查看试题解析
17. 如图，在平面直角坐标系中，函数y $= \frac{\sqrt{5}}{x}$ （x＞0）与y＝x﹣2的图像交于点P（a，b），则代数式 $\frac{1}{a} - \frac{1}{b}$ 的值为．

查看试题解析
18. 如图，正方形ABCD的边长为8，点E、F分别在线段AB、AD上，且AF＝4，AE＝3，若点P，Q分别在线段BC、CD上运动，G为线段PF上的点，在运动过程中，始终保持∠GEB＝∠GFA，则线段GQ的最小值为．

查看试题解析

三、解答题

19. 如图，一个可以自由转动的转盘被均匀分成3等份，每份分别标上数字﹣3，0，2．现做一个游戏，小黄先转动转盘一次，转盘停止后，指针指向的数字记为x，小林再转动转盘一次，转盘停止后，指针指向的数字记为y，从而得到A（x，y）．（注：若指针停在等分线处，则重新转动．）

(1)、用列表或画树状图的方法列出所有可能的点A的坐标；

(2)、若规定点A（x，y）在第一象限内小黄获胜，点A（x，y）在第三象限内小林获胜，此游戏公平吗？并说明理由．

查看试题解析
20. 如图，在Rt△ABC中，∠BAC＝90°，∠ACB＝30°，将△ABC绕点C逆时针旋转60°得到△CDE，点A、B的对应点分别是D、E，点F是边BC中点，连结AD、EF．

(1)、求证：△ACD是等边三角形；

(2)、判断AD与EF有怎样的数量关系，并说明理由．

查看试题解析
21. 某商店销售一种成本为30元/千克的商品，若按40元/千克销售，一个月可售出600千克，现采用提高售价的办法增加利润，已知这种商品每涨价1元，月销售量就减少10千克．

(1)、商店应将售价定为多少元，才能使月销售的利润为10000元？

(2)、若规定该商品的利润率不低于50%但不超过100%，当售价定为多少时，月销售的利润可达到最大值？最大值为多少？

查看试题解析
22. 如图，AB为⊙O的直径，点D为圆外一点，连接AD、BD，分别与⊙O相交于点C、E，且 $\hat{A C} = \hat{C E}$ ，过点C作CF⊥BD于点F，连接BC．

(1)、求证：CF是⊙O的切线；

(2)、若∠CBD＝30°，AC＝5，求阴影部分面积（结果保留π）．

查看试题解析
23. 如图，一次函数y＝k₁x﹣4的图象与反比例函数y $= \frac{k_{2}}{x}$ （x＞0）的图象相交于A（3，﹣6），并与x轴交于点B，点D是线段AB上一点，连结OD、OA，且S△BOD：S△BOA＝1：3．

(1)、求一次函数与反比例函数解析式；

(2)、求点D的坐标；

(3)、若将△BOD绕点O逆时针旋转，得到△B'OD'，其中点D'落在x轴的正半轴上，判断点B'是否落在反比例函数y $= \frac{k_{2}}{x}$ （x＞0）图象上，并说明理由．

查看试题解析
24. 如图1，抛物线y＝x²+bx+c与x轴交于点A（﹣3，0），B（1，0），与y轴交于点D，顶点为C，直线BC交y轴于点E．

(1)、求抛物线的解析式；

(2)、如图2，将△OBE沿直线BC平移得到△FGH．
①当点F落在抛物线上时，求点F的坐标．
②在△FGH移动过程中，是否存在点F，使得△ACF是以AC为直角边的直角三角形？若存在，请求出点F的坐标，若不存在，请说明理由．

查看试题解析