广东省惠州市惠城区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 下列图形既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将抛物线y=﹣2x2向右平移2个单位,在向上平移3个单位,所得抛物线为( )A、y=﹣2(x﹣2)2﹣3 B、y=﹣2(x+2)2+3 C、y=﹣2(x+2)2﹣3 D、y=﹣2(x﹣2)2+33. 已知m,n是方程x2+2x﹣5=0的两个实数根,则下列选项不正确的是( )A、m+n=﹣2 B、mn=﹣5 C、m2+2m﹣5=0 D、m2+2n﹣5=04. 某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ).A、20% B、40% C、18% D、36%5. 如图,AB是⊙的直径,AC是⊙的切线,A为切点,BC与⊙交于点D,连结OD.若 , 则∠AOD的度数为( )
2. 将抛物线y=﹣2x2向右平移2个单位,在向上平移3个单位,所得抛物线为( )A、y=﹣2(x﹣2)2﹣3 B、y=﹣2(x+2)2+3 C、y=﹣2(x+2)2﹣3 D、y=﹣2(x﹣2)2+33. 已知m,n是方程x2+2x﹣5=0的两个实数根,则下列选项不正确的是( )A、m+n=﹣2 B、mn=﹣5 C、m2+2m﹣5=0 D、m2+2n﹣5=04. 某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ).A、20% B、40% C、18% D、36%5. 如图,AB是⊙的直径,AC是⊙的切线,A为切点,BC与⊙交于点D,连结OD.若 , 则∠AOD的度数为( ) A、40° B、50° C、80° D、100°6. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
A、40° B、50° C、80° D、100°6. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )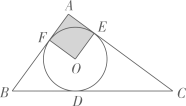 A、4 B、6.25 C、7.5 D、97. 从甲、乙、丙三人中任选两人参加“青年志愿者”活动,甲被选中的概率为( )A、 B、 C、 D、8. 若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数的图象上,则y1 , y2 , y3的大小关系是( )A、y3<y2<y1 B、y2<y1<y3 C、y1<y3<y2 D、y1<y2<y39. 若二次函数的x与y的部分对应值如下表:
A、4 B、6.25 C、7.5 D、97. 从甲、乙、丙三人中任选两人参加“青年志愿者”活动,甲被选中的概率为( )A、 B、 C、 D、8. 若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数的图象上,则y1 , y2 , y3的大小关系是( )A、y3<y2<y1 B、y2<y1<y3 C、y1<y3<y2 D、y1<y2<y39. 若二次函数的x与y的部分对应值如下表:x
-2
-1
0
1
2
3
y
14
7
2
-1
-2
-1
则当时,y的值为( )
A、-1 B、2 C、7 D、1410. 已知k1<0<k2 , 则函数和 的图象大致是( )A、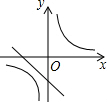 B、
B、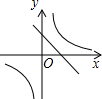 C、
C、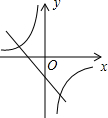 D、
D、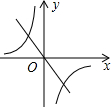
二、填空题
-
11. 方程x2=3x的根是 .12. 若关于 的一元二次方程 有实数根,则 的值可以为(写出一个即可).13. 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为 ,由此可知铅球推出的距离是m.
 14. 如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点A′落在直线BC上,连接AB′,若∠ACB=45°,AC=3,BC=2,则AB′的长为 .
14. 如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点A′落在直线BC上,连接AB′,若∠ACB=45°,AC=3,BC=2,则AB′的长为 . 15. 一圆锥的底面半径为2,母线长为3,则这个圆锥的侧面积为.16. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数上,顶点B在反比例函数上,点C在x轴的正半轴上,则平行四边形OABC的面积是 .
15. 一圆锥的底面半径为2,母线长为3,则这个圆锥的侧面积为.16. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数上,顶点B在反比例函数上,点C在x轴的正半轴上,则平行四边形OABC的面积是 .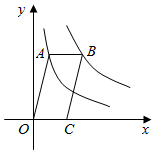 17. 二次函数 的图象如图所示,下列结论:① ;② ;③一元二次方程 有两个不相等的实数根;④当 或 时, .上述结论中正确的是 . (填上所有正确结论的序号)
17. 二次函数 的图象如图所示,下列结论:① ;② ;③一元二次方程 有两个不相等的实数根;④当 或 时, .上述结论中正确的是 . (填上所有正确结论的序号)
三、解答题
-
18. 解方程:x2﹣4x﹣5=0.19. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0)、A(4,1)、B(4,4)均在格点上.
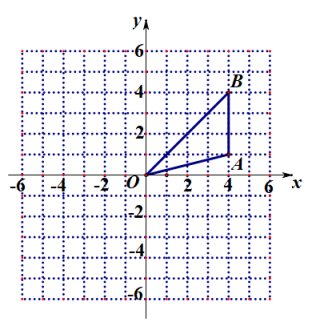 (1)、画出△OAB绕原点顺时针旋转后得到的△ , 并写出点的坐标;(2)、在(1)的条件下,求线段在旋转过程中扫过的扇形的面积.20. 如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5°,AB=2.求半径OB的长.
(1)、画出△OAB绕原点顺时针旋转后得到的△ , 并写出点的坐标;(2)、在(1)的条件下,求线段在旋转过程中扫过的扇形的面积.20. 如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5°,AB=2.求半径OB的长.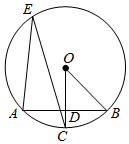 21. 如图,反比例函数和一次函数y=kx-1的图象相交于A(m,2m),B两点.
21. 如图,反比例函数和一次函数y=kx-1的图象相交于A(m,2m),B两点. (1)、求一次函数的表达式;(2)、求出点B的坐标,并根据图象直接写出满足不等式的x的取值范围.22. 甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用x、y表示.若x+y为奇数,则甲获胜;若x+y为偶数,则乙获胜.(1)、用列表法或树状图法(树状图也称树形图)中的一种方法,求(x,y)所有可能出现的结果总数;(2)、你认为这个游戏对双方公平吗?请说明理由.23. 新冠疫情期间,某网店以100元/件的价格购进一批消毒用紫外线灯,该网店店主结合店铺数据发现,日销量y(件)是售价x(元/件)的一次函数,其售价和日销售量的四组对应值如表:
(1)、求一次函数的表达式;(2)、求出点B的坐标,并根据图象直接写出满足不等式的x的取值范围.22. 甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用x、y表示.若x+y为奇数,则甲获胜;若x+y为偶数,则乙获胜.(1)、用列表法或树状图法(树状图也称树形图)中的一种方法,求(x,y)所有可能出现的结果总数;(2)、你认为这个游戏对双方公平吗?请说明理由.23. 新冠疫情期间,某网店以100元/件的价格购进一批消毒用紫外线灯,该网店店主结合店铺数据发现,日销量y(件)是售价x(元/件)的一次函数,其售价和日销售量的四组对应值如表:售价x(元/件)
150
160
170
180
日销售量y(件)
200
180
160
140
另外,该网店每日的固定成本折算下来为2000元.
注:日销售纯利润=日销售量×(售价﹣进价)﹣每日固定成本
(1)、求y关于x的函数解析式(不要求写出自变量的取值范围);(2)、日销售纯利润为W(元),求出W与x的函数表达式;(3)、当售价定为多少元时,日销售纯利润最大,最大纯利润是多少.24. 如图,AB是⊙O的弦,过点O作OC⊥OA,OC交AB于P,CP=BC,点Q是上的一点.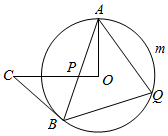 (1)、求证:BC是⊙O的切线;(2)、已知∠BAO=25°,求∠AQB的度数;(3)、在(2)的条件下,若OA=18,求的长.25. 已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点,过点P作x轴的垂线,交线段AB于点D,再过点P作PEx轴交抛物线于点E.
(1)、求证:BC是⊙O的切线;(2)、已知∠BAO=25°,求∠AQB的度数;(3)、在(2)的条件下,若OA=18,求的长.25. 已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点,过点P作x轴的垂线,交线段AB于点D,再过点P作PEx轴交抛物线于点E.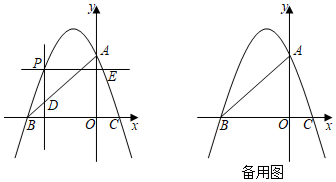 (1)、求抛物线解析式;(2)、当点P运动到什么位置时,DP的长最大?(3)、是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
(1)、求抛物线解析式;(2)、当点P运动到什么位置时,DP的长最大?(3)、是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.