广东省广州市海珠区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知 $△$ ABO∽ $△$ DEO，且BO：EO＝1：3，则△ABO与△DEO的面积比是（）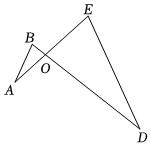

A、1：3 B、3：1 C、1：9 D、9：1

查看试题解析
3. 如图，抛物线对称轴为直线x＝1，与x轴交于点A(﹣1，0)，则另一交点的坐标是（）

A、(3，0) B、(﹣3，0) C、(1，0) D、(2，0)

查看试题解析
4. 社区医院十月份接种了新冠疫苗100份，十二月份接种了392份．设该社区医院平均每月接种疫苗的增长率为x，那么x满足的方程是（）

A、100（1+x）²＝392 B、392（1﹣x）²＝100 C、100（1+2x）²＝392 D、100（1+x²）＝392

查看试题解析
5. 已知：如图，在△ABC中，∠ADE＝∠C，则下列等式成立的是（）

A、 $\frac{A D}{A B} = \frac{A E}{A C}$ B、 $\frac{A E}{B C} = \frac{A D}{B D}$ C、 $\frac{D E}{B C} = \frac{A E}{A B}$ D、 $\frac{D E}{B C} = \frac{A D}{A B}$

查看试题解析
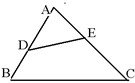6. 如何平移抛物线y＝﹣（x+4）²﹣1得到抛物线y＝﹣x²（）

A、先向左平移4个单位，再向下平移1个单位 B、先向右平移4个单位，再向上平移1个单位 C、先向左平移1个单位，再向下平移4个单位 D、先向右平移1个单位，再向上平移4个单位

查看试题解析
7. 若关于x的一元二次方程（m+1）x²+3x+m²﹣1＝0的一个实数根为0，则m等于（）

A、1 B、±1 C、﹣1 D、0

查看试题解析
8. 如图，在⊙O中，CD是⊙O的直径，AB⊥CD于点E，若AB＝8，CE＝2，则⊙O的半径为（）

A、 $2 \sqrt{5}$ B、 $\sqrt{5}$ C、3 D、5

查看试题解析
9. 如图，PA、PB切⊙O于点A、B，直线FG切⊙O于点E，交PA于F，交PB于点G，若PA＝8cm，则△PFG的周长是（）

A、8cm B、12cm C、16cm D、20cm

查看试题解析
10. 如图， $△ A B C$ 中， $A B = A C ， B C = 6 ， A D ⊥ B C$ 于点 $D ， A D = 4 ， P$ 是半径为2的 $⊙ A$ 上一动点，连结 $P C$ ，若 $E$ 是 $P C$ 的中点，连结 $D E$ ，则 $D E$ 长的最大值为（）

A、3 B、 $3.5$ C、4 D、 $4.5$

查看试题解析

二、填空题

11. 函数y＝x²﹣5的最小值是．

查看试题解析
12. 如图， $A 、 B 、 C$ 是 $⊙ O$ 上的三点，则 $∠ A O B = 80 °$ ，则 $∠ A C B =$ 度.

查看试题解析
13. 圆锥底面的半径为5cm，高为12cm，则圆锥的侧面积为cm² ．

查看试题解析
14. 二次函数y＝（x﹣1）² ，当x＜1时，y随x的增大而（填“增大”或“减小”）．

查看试题解析
15. 如图，半圆的圆心与坐标原点重合，半圆的半径1，直线 $l$ 的解析式为 $y = x + t$ 若直线 $l$ 与半圆只有一个交点，则t的取值范围是．

查看试题解析
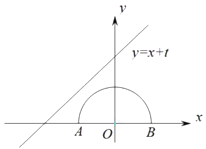16. 如图，在 $△$ ABC中，AB＝AC，以AB为直径的半圆O交BC于点D，交AC于点E，连接AD、BE交于点M，过点D作DF⊥AC于点F，DH⊥AB于点H，交BE于点G：下列结论：① $△$ CDF≌ $△$ BDH，②DG＝DM，③CF＝FE，④BE＝2DH，其中正确结论的序号是．

查看试题解析

三、解答题

17. 解方程：

(1)、x²＝4x；

(2)、x（x﹣2）＝3x﹣6．

查看试题解析
18. 如图， $△$ ABC的三个顶点A、B、C都在格点上，坐标分别为(﹣2，4)、(﹣2，0)、9﹣4，1)．

(1)、画出 $△$ ABC绕着点A逆时针旋转90°得到的 $△$ AB₁C₁；

(2)、写出点B₁、C₁的坐标．

查看试题解析
19. 如图，抛物线y＝﹣（x﹣1）²+4交x轴于A、B两点，交y轴于点C．

(1)、求点A、B、C坐标；

(2)、若直线y＝kx+b经过B、C两点，直接写出不等式﹣（x﹣1）²+4＞kx+b的解集．

查看试题解析
20. 已知关于x的一元二次方程x²﹣x+2m﹣4＝0有两个实数根．

(1)、求m的取值范围；

(2)、若方程的两根满足（x₁﹣3）（x₂﹣3）＝m²﹣1，求m的值．

查看试题解析
21. 如图，D为⊙O上一点，点C是直径BA延长线上的一点，连接CD，且∠CDA＝∠CBD．

(1)、求证：CD是⊙O的切线；

(2)、若DC＝4，AC＝2，求OC的长．

查看试题解析
22. 如图，AB＝4，CD＝6，F在BD上，BC、AD相交于点E，且AB $∥$ CD $∥$ EF．

(1)、若AE＝3，求ED的长．

(2)、求EF的长．

查看试题解析
23. 如图，已知直线y＝﹣2x+m与抛物线相交于A，B两点，且点A(1，4)为抛物线的顶点，点B在x轴上．

(1)、求抛物线的解析式；

(2)、若点P是y轴上一点，当∠APB＝90°时，求点P的坐标．

查看试题解析
24. 如图，在⊙O中，AB为弦，CD为直径，且AB⊥CD，垂足为E，P为 $\overset{⌢}{A C}$ 上的动点（不与端点重合），连接PD．

(1)、求证：∠APD＝∠BPD；

(2)、利用尺规在PD上找到点I，使得I到AB、AP的距离相等，连接AD（保留作图痕迹，不写作法）．求证：∠AIP+∠DAI＝180°；

(3)、在（2）的条件下，连接IC、IE，若∠APB＝60°，试问：在P点的移动过程中， $\frac{I C}{I E}$ 是否为定值？若是，请求出这个值；若不是，请说明理由．

查看试题解析
25. 已知抛物线G：y₁＝mx²﹣（3m﹣3）x+2m﹣3，直线h：y₂＝mx+3﹣2m，其中m≠0．

(1)、当m＝1时，求抛物线G与直线h交点的坐标；

(2)、求证：抛物线G与直线h必有一个交点A在坐标轴上；

(3)、在（2）的结论下，解决下列问题：
①无论m怎样变化，求抛物线G一定经过的点坐标；
②将抛物线G关于原点对称得到的图象记为抛物线 $G'$ ，试结合图象探究：若在抛物线G与直线h，抛物线 $G'$ 与直线h均相交，在所有交点的横坐标中，点A横坐标既不是最大值，也不是最小值，求此时抛物线G的对称轴的取值范围．

查看试题解析