广东省广州市白云区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案中，是中心对称图形的是（）．

A、 B、 C、 D、

查看试题解析
2. 在下图的各事件中，是随机事件的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图，PA、PB是⊙O的切线，切点是A、B，已知∠P=60°，OA=3，那么∠AOB所对弧的长度为（）

A、6π B、5π C、3π D、2π

查看试题解析
4. 如果反比例函数 $y = \frac{1 - 2 m}{x}$ 的图象在所在的每个象限内y都是随着x的增大而减小，那么m的取值范围是（）

A、m＞ $\frac{1}{2}$ B、m＜ $\frac{1}{2}$ C、m≤ $\frac{1}{2}$ D、m≥ $\frac{1}{2}$

查看试题解析
5. 方程 $x^{2} + 8 x + 17 = 0$ 的根的情况是（）．

A、没有实数根 B、有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
6. 点 $(3 ， - 2)$ 在反比例函 $y = \frac{k}{x}$ 的图象上，则下列说法正确的是（）

A、 $k = 6$ B、函数的图象关于 $y = x$ 对称 C、函数的图象经过点（6，1） D、函数的图象关于原点对称

查看试题解析
7. 如图⊙O的直径 $A B$ 垂直于弦 $C D$ ，垂足是 $E$ ， $∠ A = 22.5 °$ ， $O C = 4$ ， $C D$ 的长为（）

A、 $2 \sqrt{2}$ B、4 C、 $4 \sqrt{2}$ D、8

查看试题解析
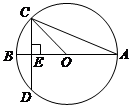8. 用一条长40cm的绳子围成一个面积为64cm²的长方形.设长方形的长为xcm，则可列方程为（）

A、x（20+x）=64 B、x（20﹣x）=64 C、x（40+x）=64 D、x（40﹣x）=64

查看试题解析
9. 如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若圆的半径为 $r$ ，扇形的圆心角等于120°，则围成的圆锥模型的高为（）．

A、 $2 \sqrt{2} r$ B、 $3 r$ C、 $\sqrt{10} r$ D、 $\sqrt{35} r$

查看试题解析
10. 已知抛物线 $y = a x^{2} - b x + c$ 如图，下列说法：① $a + b + c = 0$ ， ② $a - b + c > 0$ ， ③ $b > 0$ ， ④ $c = - 1$ ，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 抛物线 $y = x^{2} - 2 x + 3$ 有最点（填写“高”或“低”），这个点的坐标是．

查看试题解析
12. 点A是反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限内的图象上一点，过点A作 $A B ⊥ x$ 轴，垂足为点B， $△ O A B$ 的面积是1，则 $k =$ ．

查看试题解析
13. 如图是一个可以自由转动的转盘，转盘分成3个大小相同的扇形，标号分别为Ⅰ，Ⅱ，Ⅲ，三个数字，指针的位置固定，转动的转盘停止后，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，当作指向右边的扇形），指针指向扇形Ⅰ的概率是．

查看试题解析
14. 如图，AB是 $⊙ O$ 的直径， $A B = A C$ ， BC交 $⊙ O$ 于点D，AC交 $⊙ O$ 于点E， $∠ B A C = 45 °$ ，则 $∠ E B C =$ °．

查看试题解析
15. 为了估计鱼塘中的鱼数，养鱼者首先从鱼塘中打捞100条鱼，在每一条鱼身上做好记号后把这些鱼放归鱼塘，再从鱼塘中打捞10条鱼，如果在这10条鱼中有1条鱼是有记号的，那么估计鱼塘中鱼的条数为条．

查看试题解析
16. 如图，在锐角 $△ A B C$ 中， $∠ B A C = 60 °$ ， AE是中线，BF和CD是高则下列结论中，正确的是（填序号）．
① $B C = 2 D F$
② $∠ C E F = 2 ∠ C D F$
③ $△ D E F$ 是等边三角形
④ $(C F + C D) ： (B D + B F) = (B D - B F) ： (C F - C D)$ ．

查看试题解析

三、解答题

17. 解方程： ${(x + 3)}^{2} - 25 = 0$

查看试题解析
18. 一个二次函数的图象经过 $(- 1 ， 0)$ ， $(0 ， 6)$ ， $(3 ， 0)$ 三点．求：这个二次函数的解析式．

查看试题解析
19. 如图，AB为 $⊙ O$ 的直径，AC平分 $∠ B A D$ 交 $⊙ O$ 于点C， $C D ⊥ A D$ ，垂足为点D．求证：CD是 $⊙ O$ 的切线．

查看试题解析
20. 已知函数 $y = (k - 2) x^{k + 2}$ 为反比例函数．

(1)、求这个反比例函数的解析式；

(2)、这个函数的图象位于第象限；在每一个象限内，y随x的增大而；

(3)、当 $- 3 \leq x \leq - \frac{1}{2}$ 时，函数的最大值为，最小值为．

查看试题解析
21. 如图， $△ A B C$ 是以 $A B = a$ 为斜边的等腰直角三角形，其内部的4段弧均等于以BC为直径的 $\frac{1}{4}$ 圆周，求图中阴影部分的面积．

查看试题解析
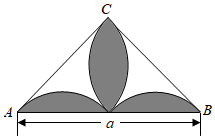22. 为落实“双减”，进一步深化白云区“数学提升工程”，提升学生数学核心素养，2021年12月3日开展“双减”背景下白云区初中数学提升工程成果展示现场会，其中活动型作业展示包括以下项目：①数独挑战；②数学谜语；③一笔画；④24点；⑤玩转魔方．为了解学生最喜爱的项目，随机抽取若干名学生进行调查，将调查结果绘制成两个不完整的统计图，如图：

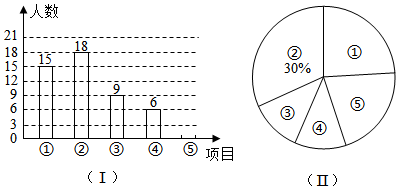(1)、本次随机抽查的学生人数为 ▲ 人，补全图（Ⅰ）；

(2)、参加活动的学生共有500名，可估计出其中最喜爱①数独挑战的学生人数为人，图（Ⅱ）中扇形①的圆心角度数为度；

(3)、计划在①，②，③，④四项活动中随机选取两项作为重点直播项日，请用列表或画树状图的方法，求恰好选中①，④这两项活动的概率

查看试题解析
23. 一个菱形两条对角线长的和是 $10 c m$ ，面积是 $12 c m^{2}$ ．求菱形的周长．

查看试题解析
24. 已知抛物线 $y = x^{2} + m x + n$ 与x轴的负、正半轴分别交于A，B两点，与y轴的负半轴交于点D点C是抛物线的顶点．

(1)、若 $O A - O B = 2$ ，求该抛物线的对称轴；

(2)、在（1）的条件下，连接AD，CD，若 $A D ⊥ C D$ ，求该抛物线的解析式；

(3)、若 $O A - O B = 2 p$ ，点D的坐标为 $(0 ， - | p |)$ ，请判断点C是否存在最高点或最低点，若存在，求该点的坐标；若不存在，请说明理由．

查看试题解析
25. 如图，已知在 $△ A B C$ 中， $∠ A$ 是钝角，以AB为边作正方形ABDE，使 $△ A B C$ 正方形ABDE分居在AB两侧，以AC为边作正方形ACFG，使 $△ A B C$ 正方形ACFG分居在AC两侧，BG与CE交于点M，连接AM．

(1)、求证 $B G = C E_{1}$ ；

(2)、求： $∠ A M C$ 的度数

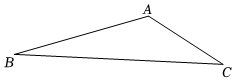(3)、若 $B G = a$ ， $M G = b$ ，求： $S_{△ A B M} ： S_{△ A C M}$ （结果可用含有a，b，c的式子表示）．

查看试题解析