广东省佛山市顺德区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 下面几个几何体,从正面看到的形状是圆的是( )A、
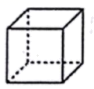 B、
B、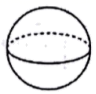 C、
C、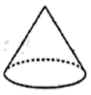 D、
D、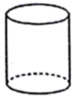 2. 若x=1是方程x2﹣4x+m=0的根,则m的值为( )A、﹣3 B、﹣5 C、3 D、53. 用配方法解方程 x2﹣6x﹣5=0,下列配方结果正确的是( )A、(x﹣6)2=41 B、(x﹣3)2=14 C、(x+3)2=14 D、(x﹣3)2=44. 如图,在△ABC中,DE∥BC,AD=4,DB=2,AE=3,则EC的长为( )
2. 若x=1是方程x2﹣4x+m=0的根,则m的值为( )A、﹣3 B、﹣5 C、3 D、53. 用配方法解方程 x2﹣6x﹣5=0,下列配方结果正确的是( )A、(x﹣6)2=41 B、(x﹣3)2=14 C、(x+3)2=14 D、(x﹣3)2=44. 如图,在△ABC中,DE∥BC,AD=4,DB=2,AE=3,则EC的长为( ) A、 B、1 C、2 D、5. 一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其它完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在20%附近,口袋中白球最有可能有( )个.A、6 B、8 C、10 D、126. 若一元二次方程ax2+bx+c=0的系数满足ac<0,则方程根的情况是( )A、没有实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、无法判断7. 正方形具有而矩形不一定有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角互补 D、四个角相等8. 已知(x1 , y1)和(x2 , y2)是反比例函数y=图象上的两个点,当x1<x2<0时,y1与y2的大小关系是( )A、y1<y2 B、y1≤y2 C、y1>y2 D、y1≥y29. 顺次连接平行四边形各边的中点得到的四边形是( )A、平行四边形 B、菱形 C、矩形 D、正方形10. 如图,矩形ABCD的边DC在x轴上,点B在反比例函数y=的图象上,点E是AD边上靠近点A的三等分点,连接CE交y轴于点F,则△CDF的面积为( )
A、 B、1 C、2 D、5. 一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其它完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在20%附近,口袋中白球最有可能有( )个.A、6 B、8 C、10 D、126. 若一元二次方程ax2+bx+c=0的系数满足ac<0,则方程根的情况是( )A、没有实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、无法判断7. 正方形具有而矩形不一定有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角互补 D、四个角相等8. 已知(x1 , y1)和(x2 , y2)是反比例函数y=图象上的两个点,当x1<x2<0时,y1与y2的大小关系是( )A、y1<y2 B、y1≤y2 C、y1>y2 D、y1≥y29. 顺次连接平行四边形各边的中点得到的四边形是( )A、平行四边形 B、菱形 C、矩形 D、正方形10. 如图,矩形ABCD的边DC在x轴上,点B在反比例函数y=的图象上,点E是AD边上靠近点A的三等分点,连接CE交y轴于点F,则△CDF的面积为( ) A、2 B、 C、 D、1
A、2 B、 C、 D、1二、填空题
-
11. 方程x2=2x的解是.12. 在Rt△ABC中,∠C=90°,AB=2AC,则∠A=°.13. 一个正方形的对角线长为2,则其面积为 .14. 如图,四边形ABCD是正方形,△CBE是等边三角形,则∠AEB=.
 15. 甲、乙两根木杆竖直立在平地上,其高度分别是2m和3m.某一时刻,甲木杆在太阳光下的影长为3m,则乙木杆的影长为m.16. 如图,在△ABC中,AB=AC=3,BC=4.若D是BC边上的黄金分割点,则△ABD的面积为 .
15. 甲、乙两根木杆竖直立在平地上,其高度分别是2m和3m.某一时刻,甲木杆在太阳光下的影长为3m,则乙木杆的影长为m.16. 如图,在△ABC中,AB=AC=3,BC=4.若D是BC边上的黄金分割点,则△ABD的面积为 . 17. 如图,在正方形ABCD中,DE=CE,AF=3DF,过点E作EG⊥BF于点H,交AD于点G.下列结论:
17. 如图,在正方形ABCD中,DE=CE,AF=3DF,过点E作EG⊥BF于点H,交AD于点G.下列结论:①△DEF∽△CBE;
②∠EBG=45°;
③AD=3AG.正确的有 .

三、解答题
-
18. 计算:sin30°+3tan60°﹣cos245°19. 将A、B、C、D四人随机分成甲乙两组参加乒乓球双打比赛,求A、B同时分在甲组的概率.20. 为满足市场需求,某工厂决定从2月份起扩大产能,其中2020年1~4月份的产量统计如图所示.求从2月份到4月份的月平均增长率.
 21. 已知A(m+3,2)和B(3,)是同一个反比例函数图象上的两个点.
21. 已知A(m+3,2)和B(3,)是同一个反比例函数图象上的两个点. (1)、求出m的值;(2)、写出反比例函数的表达式,并画出图象.22. 如图,在矩形ABCD中,AB=6,BC=8.
(1)、求出m的值;(2)、写出反比例函数的表达式,并画出图象.22. 如图,在矩形ABCD中,AB=6,BC=8. (1)、用尺规作图法作菱形AECF,使点E、F分别在BC和AD边上;(2)、求EF的长度.23. 菱形ABCD的边长为6,∠D=60°,点E在边AD上运动.
(1)、用尺规作图法作菱形AECF,使点E、F分别在BC和AD边上;(2)、求EF的长度.23. 菱形ABCD的边长为6,∠D=60°,点E在边AD上运动. (1)、如图1,当点E为AD的中点时,求AO:CO的值;(2)、如图2,F是AB上的动点,且满足BF+DE=6,求证:△CEF是等边三角形.24. 如图1,反比例函数y=的图象经过A(1,m)、B(2,1)两点,点P的坐标为(6,1).
(1)、如图1,当点E为AD的中点时,求AO:CO的值;(2)、如图2,F是AB上的动点,且满足BF+DE=6,求证:△CEF是等边三角形.24. 如图1,反比例函数y=的图象经过A(1,m)、B(2,1)两点,点P的坐标为(6,1). (1)、求反比例函数的表达式;(2)、连接PA、PB,求tan∠P的值;(3)、如图2,点C、D的坐标是(a,0)、(0,a)(0<a≤6),当△PCD的面积为3时,求a的值.25. 如图,在正方形ABCD中,E、F、G分别是AB、BC、CD边上的点,AF和EG交于点H.现在提供三个关系:①AF⊥EG;②AH=HF;③AF=EG.
(1)、求反比例函数的表达式;(2)、连接PA、PB,求tan∠P的值;(3)、如图2,点C、D的坐标是(a,0)、(0,a)(0<a≤6),当△PCD的面积为3时,求a的值.25. 如图,在正方形ABCD中,E、F、G分别是AB、BC、CD边上的点,AF和EG交于点H.现在提供三个关系:①AF⊥EG;②AH=HF;③AF=EG.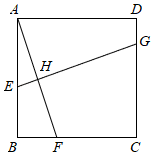 (1)、从三个关系中选择一个作为条件,一个作为结论,形成一个真命题.写出该命题并证明;(2)、若AB=3,EG垂直平分AF,设BF=n.
(1)、从三个关系中选择一个作为条件,一个作为结论,形成一个真命题.写出该命题并证明;(2)、若AB=3,EG垂直平分AF,设BF=n.①求EH:HG的值(含n的代数式表示);
②连接FG,点P在FG上,当四边形CPHF是菱形时,求n的值.