广东省佛山市三水区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 若2x=5y，则 $\frac{x}{y}$ 的值是（）

A、 $\frac{5}{2}$ B、 $\frac{2}{5}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
2. 如图所示的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列关于矩形的说法，正确的是（）．

A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、矩形的对角线互相垂直且平分 D、矩形的对角线相等且互相平分

查看试题解析
4. 连续两次掷一枚质地均匀的硬币，两次都是正面朝上的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
5. 两个相似多边形的相似比是3：4，其中小多边形的面积为18cm² ，则较大多边形的面积为（）

A、16cm² B、54cm² C、32cm² D、48cm²

查看试题解析
6. 如图， $A B / / C D / / E F$ ，若 $B F = 3 D F$ ，则 $\frac{A C}{C E}$ 的值是（）

A、2 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、3

查看试题解析
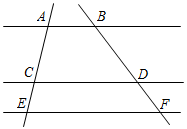7. 点A（﹣3，y₁）、B（﹣1，y₂）、C（2，y₃）都在反比例函数y＝ $\frac{- 6}{x}$ 的图象上，则y₁、y₂、y₃的大小关系是（）

A、y₁ $<$ y₂ $<$ y₃ B、y₃ $<$ y₂ $<$ y₁ C、y₃ $<$ y₁ $<$ y₂ D、y₂ $<$ y₁ $<$ y₃

查看试题解析
8. 一元二次方程x²+x﹣3=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
9. 如图，有一张矩形纸片，长10cm，宽6cm，在它的四角各减去一个同样的小正方形，然后折叠成一个无盖的长方体纸盒．若纸盒的底面（图中阴影部分）面积是32cm² ，求剪去的小正方形的边长．设剪去的小正方形边长是xcm，根据题意可列方程为（）

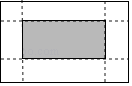A、10×6﹣4×6x=32 B、（10﹣2x）（6﹣2x）=32 C、（10﹣x）（6﹣x）=32 D、10×6﹣4x²=32

查看试题解析
10. 函数y=x+m与 $y = \frac{m}{x}$ $(m \neq 0)$ 在同一坐标系内的图象可以是（）

A、 B、 C、 D、

查看试题解析
11. 如图，在平面直角坐标系中，已知点A（﹣3，6）、B（﹣9，﹣3），以原点O为位似中心，相似比为 $\frac{1}{3}$ ，把△ABO缩小，则点B的对应点B′的坐标是（）

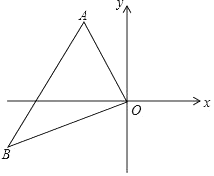A、（﹣3，﹣1） B、（﹣1，2） C、（﹣9，1）或（9，﹣1） D、（﹣3，﹣1）或（3，1）

查看试题解析
12. 如图，在矩形ABCD中，对角线 $A C$ 、BD交于C， $B C = 2 ， A E ⊥ B D$ ，垂足为E， $∠ B A E = 30 °$ ，那么 $Δ E C O$ 的面积是（）

A、 $\frac{2 \sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{6}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{9}$

查看试题解析

二、填空题

13. 在某一时刻，测得一根长为1.5m的标杆的影长为3m，同时测得一根旗杆的影长为16m，那么这根旗杆的高度为m．

查看试题解析
14. 一个不透明袋中装有若干个红球，为估计袋中红球的个数，小文在袋中放入10个白球（每个球除颜色外其余都与红球相同）.摇匀后每次随机从袋中摸出一个球，记下颜色后放回袋中，通过大量重复摸球试验后发现，摸到白球的频率是 $\frac{2}{7}$ ，则袋中红球约为个.

查看试题解析
15. 若一元二次方程ax²﹣bx﹣2021=0有一根为x=﹣1，则a+b= ．

查看试题解析
16. 如图，小明为了测量树的高度CD，他在与树根同一水平面上的B处放置一块平面镜，然后他站在A处刚好能从镜中看到树顶D，已知A、B、C三点在同一直线上，且AB＝2m，BC＝8m．他的眼睛离地面的高度1.6m，则树的高度CD为m．

查看试题解析
17. 如图，点O是菱形ABCD对角线的交点，DE $/ /$ AC，CE $/ /$ BD，连接OE，设AC＝12，BD＝16，则OE的长为．

查看试题解析
18. 如图，矩形ABCD的顶点A和对称中心均在反比例函数y＝ $\frac{k}{x}$ （k≠0，x＞0）上，若矩形ABCD的面积为8，则k的值为.

查看试题解析

三、解答题

19. 已知关于x的方程x²+ax+a﹣2＝0．

(1)、若该方程的一个根为1，求a的值；

(2)、若a的值为3时，请解这个方程．

查看试题解析
20. 某数学小组为调查重庆实验外国语学校周五放学时学生的回家方式，随机抽取了部分学生进行调查，所有被调查的学生都需从“ $A$ ：乘坐电动车， $B$ ：乘坐普通公交车或地铁， $C$ ：乘坐学校的定制公交车， $D$ ：乘坐家庭汽车， $E$ ：步行或其他”这五种方式中选择最常用的一种，随后该数学小组将所有调查结果整理后绘制成如图不完整的条形统计图和扇形统计图，请结合统计图回答下列问题．

(1)、本次调查中一共调查了名学生；扇形统计图中， $E$ 选项对应的扇形圆心角是度；

(2)、请补全条形统计图；

(3)、若甲、乙两名学生放学时从 $A$ 、 $B$ 、 $C$ 三种方式中随机选择一种，请用列表法或画树状图的方法，求出甲、乙两名学生恰好选择同一种交通工具上班的概率．

查看试题解析
21. 深圳市某商场销售某女款上衣，刚上市时每件可盈利100元，销售一段时间后开始滞销，经过连续两次降价后，每件盈利为81元，平均每天可售出20件．

(1)、求平均每次降价盈利的百分率；

(2)、为扩大销售量，尽快减少库存，在“双十一”期间该商场决定再次采取适当的降价措施，经调查发现，一件女款上衣每降价1元，每天可多售出2件．若商场每天要盈利2940元，每件应降价多少元？

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，垂足为F，交直线MN于E，连接CD，BE．

(1)、求证：CE＝AD；

(2)、当D为AB中点时，四边形BECD是什么特殊四边形？说明你的理由；

(3)、在满足（2）的条件下，当△ABC满足什么条件时，四边形BECD是正方形？（不必说明理由）

查看试题解析
23. 如图1，一次函数y＝kx﹣3（k≠0）的图象与y轴交于点B，与反比例函数y＝ $\frac{m}{x}$ （x＞0）的图象交于点A（8，1）．

(1)、求出一次函数与反比例函数的解析式；

(2)、点C是线段AB上一点（不与A，B重合），过点C作y轴的平行线与该反比例函数的图象交于点D，连接OC，OD，AD，当CD等于6时，求点C的坐标和△ACD的面积；

(3)、在（2）的前提下，将△OCD沿射线BA方向平移一定的距离后，得到△O'CD'，若点O的对应点O'恰好落在该反比例函数图象上（如图2），求出点O'，D'的坐标．

查看试题解析
24. 如图（1），在四边形ABCD中，AB∥DC，CB⊥AB，AB＝16cm，BC＝6cm，CD＝8cm，动点P从点D开始沿DA边匀速运动，动点Q从点A开始沿AB边匀速运动，它们的运动速度均为2cm/s．点P和点Q同时出发，设运动的时间为t（s），0＜t＜5

(1)、用含t的代数式表示AP；

(2)、当以点A、P、Q为顶点的三角形与△ABD相似时，求t的值；

(3)、如图（2），延长QP、BD，两延长线相交于点M，当△QMB为直角三角形时，求t的值．

查看试题解析