广东省佛山市南海区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中没有实数根的是（）

A、 $x^{2} - 2 x + 2 = 0$ B、 $x^{2} - 4 x + 4 = 0$ C、 $x (x - 2) = 0$ D、 ${(x - 1)}^{2} = 3$

查看试题解析
2. 矩形、菱形都具有的性质是（）

A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、对角线互相垂直且相等

查看试题解析
3. 已知反比例函数 $y = \frac{k}{x}$ 经过点A $(3 ， 2)$ 、B $(- 1 ， m)$ ，则m的值为（）

A、-6 B、 $- \frac{2}{3}$ C、 $\frac{2}{3}$ D、6

查看试题解析
4. 身高1.6m的小刚在阳光下的影长是1.2m，在同一时刻，阳光下旗杆的影长是15m，则旗杆高为（）

A、14米 B、16米 C、18米 D、20米

查看试题解析
5. 在一个不透明纸箱中放有除了数字不同外，其它完全相同的2张卡片，分别标有数字1、2，从中任意摸出一张，放回搅匀后再任意摸出一张，两次摸出的数字之和为奇数的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
6. 如图，D为△ABC中AC边上一点，则添加下列条件不能判定△ABC∽△BDC的是（）

A、 $B C^{2} = A C \cdot C D$ B、 $\frac{A B}{A C} = \frac{B D}{B C}$ C、∠ABC=∠BDC D、∠A=∠CBD

查看试题解析
7. 用小正方体搭一个几何体，使它的主视图和俯视图如图所示，这样的几何体最少需要正方体个数为a，最多需要正方体个数为b，则a+b的值为（）

A、14 B、15 C、16 D、17

查看试题解析
8. 已知 $\frac{\sqrt{5} + 1}{2}$ 是一元二次方程 $x^{2} - x + m = 0$ 的一个根，则方程的另外一根为（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{3 - \sqrt{5}}{2}$ C、 $\frac{1 - \sqrt{5}}{2}$ D、 $\frac{\sqrt{5} - 3}{2}$

查看试题解析
9. 2002年国际数学家大会在北京召开，大会的会标是我国古代数学家赵爽画的“弦图”（如图），体现了数学研究的继承和发展，弦图中四边形ABCD与EFGH均为正方形，若 $A G = B H = C E = D F = a ，$ $A F = B G = C H = D E = b ，$ 且正方形EFGH的面积为正方形ABCD的面积的一半，则a：b的值为（）

A、 $2 - \sqrt{3}$ B、 $\sqrt{2}$ C、2 D、 $2 + \sqrt{3}$

查看试题解析
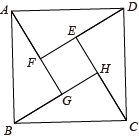10. 如图，已知E，F分别为正方形ABCD的边AB、BC的中点，AF与DE交于点M，则下列结论：①AF⊥DE；② $A E = E G$ ；③AM= $\frac{2}{3}$ MF；④ $\frac{S_{Δ A E M}}{S_{Δ A D M}} = \frac{1}{4}$ ．其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 已知 $\frac{a}{b} = \frac{3}{2}$ ，则 $\frac{a + b}{a - b}$ = ．

查看试题解析
12. 矩形ABCD的对角线AC和BD相交于点O，∠ACB=40°，则∠AOB=°．

查看试题解析
13. 一个不透明的袋子中放有若干个红球，小亮往其中放入10个黑球，并采用以下实验方式估算其数量：每次摸出一个小球记录下颜色并放回，实验数据如下表：
实验次数
100
200
300
400
摸出红球
78
161
238
321
则袋中原有红色小球的个数约为个．

查看试题解析
14. 正比例函数 $y_{1} = - 2 x$ 和反比例函数 $y_{2} = \frac{k}{x}$ 的图象都经过点A(-1， 2)，若 $y_{1} > y_{2}$ ，则x的取值范围是．

查看试题解析
15. 已知 $2 x^{2} - 3 x - 2 = 0$ ．则 $x^{2} + \frac{1}{x^{2}} =$ ．

查看试题解析
16. 如图，菱形ABCD边长为4，∠B=60°， $D E = \frac{1}{4} A D$ ， $B F = \frac{1}{4} B C$ ，连接EF交菱形的对角线AC于点O，则图中阴影部分面积等于．

查看试题解析
17. 如图，△ABC中AB=AC，A (0，8)，C (6，0)，D为射线AO上一点，一动点P从A出发，运动路径为A→D→C，点P在AD上的运动速度是在CD上的 $\frac{5}{3}$ 倍，要使整个运动时间最少，则点D的坐标应为．

查看试题解析

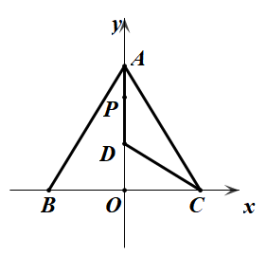
三、解答题

18. 解方程： $(x + 3) (x - \sqrt{3}) = x - \sqrt{3}$ ．

查看试题解析
19. 小明家客厅里装有一种三位单极开关，分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯，按下任意一个开关均可打开对应的一盏电灯，因刚搬进新房不久，不熟悉情况.

(1)、若小明任意按下一个开关，则小明打开走廊灯的概率是多少？

(2)、若任意按下一个开关后，再按下另两个开关中的一个，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图法或列表法加以说明.

查看试题解析
20. 如图，△ABC中，∠ACB=90°，CA=CB= $2 \sqrt{2}$ ， D、E为AB上两点，且∠DCE=45°，

(1)、求证：△ACE∽△BDC．

(2)、若AD=1，求DE的长．

查看试题解析
21. 如图，一次函数y=ax+b的图像与反比例函数 $y = \frac{k}{x}$ 的图像交于C、D两点，与x、y轴分别交于B、A两点，CE⊥x轴，且OB=4，CE=3， $\frac{C E}{B E} = \frac{1}{2}$

(1)、求一次函数的解析式和反比例函数的解析式．

(2)、求△OCD的面积．

查看试题解析
22. 为响应国家“国际国内双循环”号召，南海广场购进一批国产高档服装，进价为500元/件，售价为1000元/件时，每天可以出售40件，经市场调查发现每降价50元，一天可以多售出10件．

(1)、售价为850元时，当天的销售量为多少件？

(2)、如果每天的利润要比原来多4000元，并使顾客得到更大的优惠，问每件售价为多少元？

查看试题解析
23. 如图，公路旁有两个高度相等的路灯AB、CD，小明上午上学时发现路灯AB在太阳光下的影子恰好落在路牌底部E处，他自己的影子恰好落在路灯CD的底部C处；晚自习放学时，站在上午同一个地方，发现在路灯CD的灯光下自己的影子恰好落在E处．

(1)、在图中画出小明的位置(用线段FG表示)．

(2)、若上午上学时，高1米的木棒的影子为2米，小明身高为1.5米，他距离路牌底部E恰好2米，求路灯高．

查看试题解析
24. 如图，四边形OABC为正方形，反比例函数 $y = \frac{k}{x}$ 的图象过AB上一点E，BE=2， $\frac{A E}{O E} = \frac{3}{5}$ ．

(1)、求k的值．

(2)、反比例函数的图象与线段BC交于点D，直线y=ax+b过点D及线段AB的中点F，探究直线OF与直线DF的位置关系，并证明．

(3)、点P是直线OF上一点，当PD＋PC的值最小时，求点P的坐标．

查看试题解析
25. 如图1，在矩形ABCD中，AB＝8，AD＝4，点P是对角线BD上一点，连接AP，AE⊥AP，且 $\frac{A P}{A E} = \frac{1}{2}$ ，连接BE．

(1)、当DP=2时，求BE的长．

(2)、四边形AEBP可能为矩形吗？如果不可能，请说明理由；如果可能，求出此时四边形AEBP的面积．

(3)、如图2，作AQ⊥PE，垂足为Q，当点P从点D运动到点B时，直接写出点Q运动的距离．

查看试题解析

实验次数	100	200	300	400
摸出红球	78	161	238	321