广东省佛山市禅城区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 下列几何体中,其俯视图与主视图完全相同的是( )A、
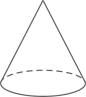 B、
B、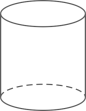 C、
C、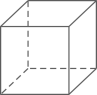 D、
D、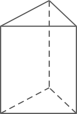 2. 如图,直线l1∥l2∥l3 , 直线AC和DF被l1 , l2 , l3所截,AB=4,BC=6,EF=9,则DE的长为( )
2. 如图,直线l1∥l2∥l3 , 直线AC和DF被l1 , l2 , l3所截,AB=4,BC=6,EF=9,则DE的长为( ) A、3 B、4 C、5 D、63. 一元二次方程x2﹣8x+5=0配方后可化为( )A、(x﹣4)=19 B、(x+4)=﹣19 C、(x﹣4)2=11 D、(x+4)2=164. 如图,D是BC上的点,∠ADC=∠BAC,则下列结论正确的是( )
A、3 B、4 C、5 D、63. 一元二次方程x2﹣8x+5=0配方后可化为( )A、(x﹣4)=19 B、(x+4)=﹣19 C、(x﹣4)2=11 D、(x+4)2=164. 如图,D是BC上的点,∠ADC=∠BAC,则下列结论正确的是( )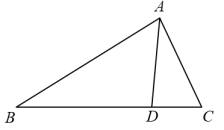 A、△ABC∽△DAB B、△ABC∽△DAC C、△ABD∽△ACD D、以上都对5. 菱形、矩形同时具有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补6. 已知y是x的反比例函数,如表给出了x与y的一些值,表中“▲”处的数为( )
A、△ABC∽△DAB B、△ABC∽△DAC C、△ABD∽△ACD D、以上都对5. 菱形、矩形同时具有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补6. 已知y是x的反比例函数,如表给出了x与y的一些值,表中“▲”处的数为( )x
﹣2
2
3
y
3
﹣3
▲
A、2 B、﹣2 C、1 D、﹣17. 六张朴克牌中2张“方块”,3张“梅花”,1张“红桃”.将这六张牌背面朝上,从中任意抽取1张,是“红桃”的概率为( )A、 B、 C、 D、8. 下列命题正确的是( )A、有一个角是直角的平行四边形是矩形 B、四条边相等的四边形是矩形 C、有一组邻边相等的平行四边形是矩形 D、对角线相等的四边形是矩形9. 如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面距离BC=1米,已知某一时刻BC在地面的影长CN=1.5米,AC在地面的影长CM=4.5米,则AB高为( )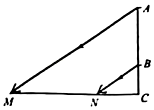 A、3.5 B、2 C、1.5 D、2.510. 若一元二次方程x2+mx+4=0有两个相等的实数根,则m的值是( )A、2 B、±2 C、±4 D、±211. 如图,一次函数y=-3x+4的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.若矩形OCPD的面积为1时,则点P的坐标为( )
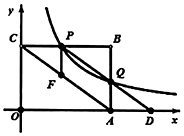
A、3.5 B、2 C、1.5 D、2.510. 若一元二次方程x2+mx+4=0有两个相等的实数根,则m的值是( )A、2 B、±2 C、±4 D、±211. 如图,一次函数y=-3x+4的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.若矩形OCPD的面积为1时,则点P的坐标为( ) A、( , 3) B、( , 2) C、( , 2)和(1,1) D、( , 3)和(1,1)12. 如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
A、( , 3) B、( , 2) C、( , 2)和(1,1) D、( , 3)和(1,1)12. 如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )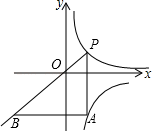 A、逐渐变大或变小 B、等于定值16 C、等于定值8 D、另有答案
A、逐渐变大或变小 B、等于定值16 C、等于定值8 D、另有答案二、填空题
-
13. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AB的长为10km,则M,C之间的距离是km.
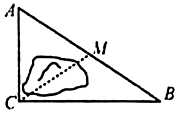 14. 已知x=﹣1是一元二次方程x2+mx+2=0的一个解,则x的值= .15. 如图,在矩形ABCD中,AD=13,AB=5,E为BC上一点,DE平分∠AEC,则CE的长为 .
14. 已知x=﹣1是一元二次方程x2+mx+2=0的一个解,则x的值= .15. 如图,在矩形ABCD中,AD=13,AB=5,E为BC上一点,DE平分∠AEC,则CE的长为 . 16. 如图,点A是反比例函数y=(x>0)图象上的一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,4)也在此函数的图象上,则a= .
16. 如图,点A是反比例函数y=(x>0)图象上的一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,4)也在此函数的图象上,则a= . 17. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,实验数据如下表:
17. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,实验数据如下表:摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
58
96
116
295
484
601
摸到白球的频率
0.58
0.64
0.58
0.59
0.605
0.601
根据数据,估计袋中黑球有个.
18. 例.求1+2+22+23+…+22008的值.解:可设S=1+2+22+23+…+22008 , 则2S=2+22+23+24+…+22009
因此2S﹣S=22009﹣1,所以1+2+22+23+…+22008=22009﹣1.
请仿照以上过程计算出:1+3+32+33+…+32022= .
三、解答题
-
19. 如图
 (1)、如图①,在8×6的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.点C坐标为(2,4),以O为位似中心,在网格图中作△A′B'C′,使△A′B'C′与△ABC位似,且位似比为1∶2,(保留作图痕迹) , 则点C'的坐标为 , 周长比C△A'B'C′∶C△ABC= .(2)、如图②,AB和DE是直立在地面上的两根立柱.AB=6m,某一时刻AB在阳光下的投影BC=4m,DE在阳光下的投影长为6cm.请你在图中②画出此时DE在阳光下的投影EF.根据题中信息,求得立柱DE的长为 ▲ m.20. 在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,蓝球1个,若从中任意摸出一个球,摸到球是黄球的概率为 .(1)、求袋中黄球的个数;(2)、第一次任意摸出一个球(不放回),第二次再摸出一个球,求两次摸到球的颜色一次是红色、另一次是黄色的(第一次可能是红色也可能是黄球)概率.21. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)、求证:△ADF∽△DEC;(2)、若AE=6,AD=8,AB=7,求AF的长.
(1)、如图①,在8×6的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.点C坐标为(2,4),以O为位似中心,在网格图中作△A′B'C′,使△A′B'C′与△ABC位似,且位似比为1∶2,(保留作图痕迹) , 则点C'的坐标为 , 周长比C△A'B'C′∶C△ABC= .(2)、如图②,AB和DE是直立在地面上的两根立柱.AB=6m,某一时刻AB在阳光下的投影BC=4m,DE在阳光下的投影长为6cm.请你在图中②画出此时DE在阳光下的投影EF.根据题中信息,求得立柱DE的长为 ▲ m.20. 在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,蓝球1个,若从中任意摸出一个球,摸到球是黄球的概率为 .(1)、求袋中黄球的个数;(2)、第一次任意摸出一个球(不放回),第二次再摸出一个球,求两次摸到球的颜色一次是红色、另一次是黄色的(第一次可能是红色也可能是黄球)概率.21. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)、求证:△ADF∽△DEC;(2)、若AE=6,AD=8,AB=7,求AF的长. 22. 某种商品的标价为75元/件,经过两次降价后的价格为48元/件,并且两次降价的百分率相同.(1)、求该种商品每次降价的百分率;(2)、商场将进货价这30元的台灯以40元售出,平均每月能售出600个,调查表明:售价在40~60元(包含40元和60元),这种台灯的售价每上涨1元,其销售量就将减少10个.为了实现平均每月10000元的销售利润,这种台灯的售价定为多少?这时应进台灯多少个?(3)、当台灯的售价为多少时,获得的利润最大?
22. 某种商品的标价为75元/件,经过两次降价后的价格为48元/件,并且两次降价的百分率相同.(1)、求该种商品每次降价的百分率;(2)、商场将进货价这30元的台灯以40元售出,平均每月能售出600个,调查表明:售价在40~60元(包含40元和60元),这种台灯的售价每上涨1元,其销售量就将减少10个.为了实现平均每月10000元的销售利润,这种台灯的售价定为多少?这时应进台灯多少个?(3)、当台灯的售价为多少时,获得的利润最大?