广东省潮州市潮安区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 我国汽车工业迅速发展，国产汽车技术成熟，下列汽车图标是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 二次函数 $y = 2 {(x - 3)}^{2}$ 的顶点坐标为（）．

A、 $(3 ， 0)$ B、 $(- 3 ， 0)$ C、 $(0 ， - 3)$ D、 $(0 ， 3)$

查看试题解析
3. 已知点 $A (- 2 ， 3)$ 与点 $B (a ， - 3)$ 关于原点对称，则a的值为（）．

A、-2 B、-3 C、3 D、2

查看试题解析
4. 下列事件为不可能事件的是（）．

A、打开电视，正在播放广告 B、明天太阳从东方升起 C、任意画一个四边形，其内角和是180° D、投掷飞镖一次，命中靶心

查看试题解析
5. 如图，在 $⊙ O$ 中，点A，B，C在圆上， $∠ A C B = 45 °$ ，则 $△ A O B$ 的形状是（）．

A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形

查看试题解析
6. 某鱼塘里养了若干条草鱼、100条鲤鱼和50条罗非鱼，通过多次捕捞实验后发现，捕捞到草鱼的频率稳定在0.5左右．可估计该鱼塘中鱼的总数量为（）．

A、300 B、200 C、150 D、250

查看试题解析
7. 某厂家2020年1～5月份的口罩产量统计如图所示.设从2月份到4月份，该厂家口罩产量的平均月增长率为x，根据题意可得方程（　　）

A、180（1﹣x）²=461 B、180（1+x）²=461 C、368（1﹣x）²=442 D、368（1+x）²=442

查看试题解析
8. 定义运算： $m △ n = m n^{2} - 2 m n - 1$ ．例如： $4 △ 2 = 4 \times 2^{2} - 2 \times 4 \times 2 - 1 = - 1$ ．则方程 $2 △ x = 0$ 的根的情况为（）．

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、以上结论都不对

查看试题解析
9. 如图，正五边形ABCDE边长为6，以A为圆心，AB为半径画圆，图中阴影部分的面积为（）．

A、 $\frac{18}{5} π$ B、 $4 π$ C、 $\frac{54}{5} π$ D、 $12 π$

查看试题解析
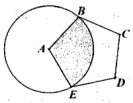10. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的对称轴为直线 $x = - 1$ ，下列结论中，其中结论正确的是（）．
① $a b c < 0$ ；② $2 a - b = 0$ ；③ $3 a < - c$ ；④若m为任意实数，则有 $a - b m \leq a m^{2} + b$ ；
⑤若图象经过点 $(- 3 ， - 2)$ ，方程 $a x^{2} + b x + c + 2 = 0$ 的两根为 $x_{1}$ ， $x_{2} (| x_{1} | < | x_{2} |)$ ，则 $2 x_{1} - x_{2} = 5$ ．

A、①②③ B、②③④ C、②③⑤ D、③④⑤

查看试题解析

二、填空题

11. 二次函数 $y = 2 x^{2}$ 向上平移2个单位后的解析式为．

查看试题解析
12. 在单词 $m a t h e m a t i c s$ （数学）中任意选择一个字母，选中字母“a”的概率为．

查看试题解析
13. 我国南宋数学家杨辉所著《田亩比类乘除捷法》中记载了这样一道题：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步．”其大意为：一个矩形的面积为864平方步，宽比长少12步，问宽和长各多少步？设矩形的宽为x步，根据题意，可列方程为．

查看试题解析
14. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 40 °$ ．将 $△ A B C$ 绕点B逆时针旋转得到 $△ A' B C'$ ，使点C的对应点 $C'$ 恰好落在边AB上，则 $∠ B A' A$ 的度数是．

查看试题解析
15. 已知 $x = 0$ 是一元二次方程 $(m - 2) x^{2} + 4 x - m^{2} + 4 = 0$ 的一个根，则m的值为．

查看试题解析
16. 如图，PA，PB分别切 $⊙ O$ 于点A，B， $∠ P = 70 °$ ，若点C在 $⊙ O$ 上，且不与A，B重合，则 $∠ A C B$ 的度数是．

查看试题解析
17. 如图， $△ A B C$ 和 $△ C D E$ 都是等边三角形， $A B > C D$ ， $A B = 6$ ，固定 $△ A B C$ ，把 $△ C D E$ 绕点C旋转任意角度，连接AD，BE，设AD，BE所在的直线交于点O，则在旋转过程中，始终有 $A D = B E$ ，且 $∠ A O B$ 的大小保持不变，这时点O到直线AB的最大距离为．

查看试题解析

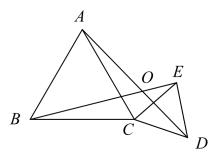
三、解答题

18. 解方程： $x^{2} - 4 x - 3 = 0$ .

查看试题解析
19. 从-2，-1，2三个数中任取两个不同的数，作为点的坐标，用列表法或画树状图求该点在第三象限的概率．

查看试题解析
20. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ，按要求完成下列问题：

(1)、作出 $△ A B C$ 的外接圆 $⊙ O$ ；（要求用尺规作图，保留作图痕迹，不要求写出作法）；

(2)、在（1）的条件下，若CD平分 $∠ A C B$ ， CD交 $⊙ O$ 于点D，连接AD，BD．求证： $A D = B D$ ．

查看试题解析
21. 如果关于x的一元二次方程 $a x^{2} + b x + c = 0$ （ $a \neq 0$ ， a，b，c是常数）有两个实数根，且其中一个根为另一个根的一半时，那么称这样的方程为“半根方程”．例如，一元二次方程 $(x - 3) (x - 6) = 0$ 的两个根是3和6，该方程可化简为 $x^{2} - 9 x + 18 = 0$ ，则方程 $x^{2} - 9 x + 18 = 0$ 就是半根方程．

(1)、请你再写出一个半根方程（要求化成一般形式）；

(2)、若关于x的方程 $(2 x - 1) (m x - n) = 0 (m \neq 0)$ 是半根方程，求 $\frac{n}{m - n}$ 的值．

查看试题解析
22. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点D在AB上， $A D = 8$ ， $B D = 6$ ， $D E ⊥ B C$ 于点E，把 $△ D B E$ 绕点D旋转得 $△ D G F$ ，且点G，F在AC上．

(1)、求证：四边形 $C E D F$ 是正方形；

(2)、求四边形 $C E D F$ 的面积，

查看试题解析
23. 某水果超市以每千克20元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于40元，经市场调查发现，樱桃的日销售量y（千克）与每千克售价x（元）满足一次函数的关系，其部分对应数据如下表所示：
每千克售价x（元）
…
25
30
35
…
日销售量y（千克）
…
110
100
90
…

(1)、求y与x之间的函数关系式，并写出自变量x的取值范围；

(2)、当每千克樱桃的售价定为多少元时，日销售利润最大？最大利润是多少？

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， D为AB边上的一点，以AD为直径的 $⊙ O$ 交BC于点E，交AC于点F，过点C作 $C G ⊥ A B$ 于点G，交AE于点H，过点E的弦EP交AB于点Q（EP不是直径），点Q为弦EP的中点，连结BP，BP恰好为 $⊙ O$ 的切线．

(1)、求证：BC是 $⊙ O$ 的切线；

(2)、求证：AE平分 $∠ C A B$ ；

(3)、若 $A Q = 10$ ， $E Q = 5$ ， $\frac{H G}{A G} = \frac{1}{2}$ ，求四边形CHQE的面积．

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 3$ 过点 $A (- 3 ， 0)$ ， $B (1 ， 0)$ ，与y轴交于点C，连接BC，点N是第一象限抛物线上一点，连接NA，交y轴于点E， $∠ N A B = ∠ B C O$ ．

(1)、求抛物线的解析式；

(2)、求线段AN的长；

(3)、若点M在第三象限抛物线上，连接MN， $∠ A N M = 45 °$ ，则这时点M的坐标为（直接写出结果）．

查看试题解析

每千克售价x（元）	…	25	30	35	…
日销售量y（千克）	…	110	100	90	…