安徽省六安市舒城县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-02-28 类型：期末考试

进入出卷网下载

一、单选题

1. 二次函数y=-（x+2）²+1的顶点坐标为（）

A、（-2，1） B、（2，1） C、（2，-1） D、（-2，-1）

查看试题解析
2. 在Rt△ABC中，∠C=90°，cosA= $\frac{2}{3}$ ，AB=6．则AC的长为（）

A、8 B、6 C、4 D、2

查看试题解析
3. 若 $\frac{x}{y} = \frac{3}{2}$ ，则 $\frac{x + y}{y}$ 的值为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{5}{2}$

查看试题解析
4. 如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB//CD，AB=2米，CD=5米，点P到CD的距离是4米，则P到AB的距离为（）

A、2.5米 B、1.6米 C、1.5米 D、1.2 米

查看试题解析
5. 若函数 $y = x^{2} - 2 x + b$ 的图象与 $x$ 轴有两个交点，则 $b$ 的取值范围是（）

A、 $b \leq 1$ B、 $b ＞ 1$ C、 $0 ＜ b ＜ 1$ D、 $b ＜ 1$

查看试题解析
6. 如图，已知∠1＝∠2，那么添加一个条件后，仍不能判定△ABC与△ADE相似的是（）

A、∠C＝∠AED B、∠B＝∠D C、 $\frac{A B}{A D} = \frac{B C}{D E}$ D、 $\frac{A B}{A D} = \frac{A C}{A E}$

查看试题解析
7. 如图1，在△ABC中，点P从点A出发向点C运动，在运动过程中，设AP=x、BP=y，y与x之间的关系如图2所示，下列结论不正确的是（）

A、AC=4 B、BC=2 $\sqrt{3}$ C、tan∠BAP= $\frac{3}{2}$ D、AB²+BC²=AC²

查看试题解析
8. 如图，在△ABC中，∠ACB=90°，AC=BC=8，将△ABC折叠，使点A落在BC边上的点D处，EF为折痕，若AE=5，则sin∠BFD的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{5}{8}$ D、 $\frac{1}{3}$

查看试题解析
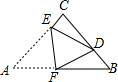9. 如图，AB⊥x轴，B为垂足，双曲线 $y = \frac{k}{x}$ （x＞0）与△AOB的两条边OA，AB分别相交于C，D两点，OC=CA，△ACD的面积为3，则k等于（）

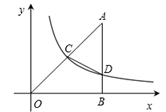A、2 B、3 C、4 D、6

查看试题解析
10. 如图，等边△ABC的边长为4cm，直线 $l$ ⊥AC所在的直线，直线 $l$ 从点A出发，以1cm/s的速度向点C运动，运动过程中与边AC相交于点M，与边AB或BC相交于点N，若△CMN的面积为y（cm），直线 $l$ 的运动时间为x（s），则下列最能反映y与x之间函数关系的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若反比例函数y= $\frac{k}{x}$ 的图象经过点（-2，6）和（4，m），则m= ．

查看试题解析
12. 如图，在四边形ABCD中，AD//BC，∠BAD=90°，且对角线BD⊥DC，AD=4，BC=9，则BD的长为．

查看试题解析
13. 如图，在平行四边形ABCD中，AC、BD相交于点O，E是OA的中点，连接BE并延长交AD于点F，则FD：AF= ．

查看试题解析
14. 如图，抛物线y=-x²+2x+c交x轴于点A（-1，0）、B（3，0），交y轴于点C，D为抛物线的顶点．

(1)、点D坐标为；

(2)、点C关于抛物线对称轴的对称点为E点，点M是抛物线对称轴上一点，且△DMB和△BCE相似，点M坐标为．

查看试题解析

三、解答题

15. 计算：cos²30°+sin²45°﹣tan60°•tan30°

查看试题解析
16. 已知二次函数的顶点坐标为A（1，9），且其图象经过点（﹣1，5）

(1)、求此二次函数的解析式；

(2)、若该函数图象与x轴的交点为B、C，求△ABC的面积．

查看试题解析
17. 如图，在边长为1的小正方形组成的网格中，△OAB的顶点都在格点上．
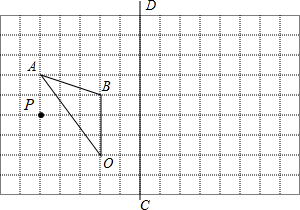
⑴请作出△OAB关于直线CD对称的△O₁A₁B₁；
⑵请以点P为中心，相似比为2，作出△OAB的同向位似图形△O₂A₂B₂ ．

查看试题解析
18. 我国首艘国产航母“山东”号是保障国土安全，维护祖国统一的又一利器．如图，一架歼15舰载机在航母正后方A点准备降落，此时在A测得航母舰首B的俯角为11.3°，舰尾C的俯角为14°，如果航空母舰长为315米且B比C高出10米，求舰载机相对舰尾C的高度（参考数据：sinl1.3°=0. 22， sin14°=0. 24，tanl1.3°=0.2，tan14° =0.25）

查看试题解析
19. 已知A（﹣4，2）、B（n，﹣4）两点是一次函数y=kx+b和反比例函数y= $\frac{m}{x}$ 图象的两个交点．

(1)、求一次函数和反比例函数的解析式；

(2)、求△AOB的面积；

(3)、观察图象，直接写出不等式 $k x + b - \frac{m}{x} > 0$ 的解集．

查看试题解析
20. 某水果经销商到水果种植基地采购葡萄，经销商一次性采购葡萄的采购单价 $y$ （元/千克）与采购量 $x$ （千克）之间的函数关系图象如图中折线 $A B \to B C \to C D$ 所示（不包括端点 $A$ ）.

(1)、当 $500 < x \leq 1000$ 时，写出 $y$ 与 $x$ 之间的函数关系式；

(2)、葡萄的种植成本为8元/千克，某经销商一次性采购葡萄的采购量不超过1000千克，当采购量是多少时，水果种植基地获利最大，最大利润是多少元？

查看试题解析
21. 如图，将矩形纸片ABCD（AD＞DC）沿着过点D的直线折叠，使点A落在BC边上，落点为E，折痕交AB边于点F．

(1)、若BE=1，EC=2，则sin∠EDC=；

(2)、若BE：EC=1：4，CD=9，求BF的长；

(3)、若BE：EC=1：m，求 AF：AB（用含有m的代数式表示）．

查看试题解析
22. 已知函数 $y_{1} = 2 k x + k$ 与函数 $y_{2} = x^{2} - 2 x + 3$ ，定义“和函数” $y = y_{1} + y_{2}$ ．

(1)、若 $k = 2$ ，则“和函数” $y =$ ；

(2)、若“和函数” $y$ 为 $y = x^{2} + b x - 2$ ，则 $k =$ ， $b =$ ；

(3)、若该“和函数” $y$ 的顶点在直线 $y = - x$ 上，求 $k$ ．

查看试题解析
23. 已知△ABC中，AC=BC，点D、E分别在AC、AB上，BD、CE交于点O．

(1)、如图①，∠ACB =60°，AD=BE，求证：∠COD=60°；

(2)、如图②，∠ACB=90°，AD= $\frac{1}{2}$ AC，AE= $\frac{1}{3}$ AB，求证：∠COD =90°；

(3)、如图③，∠ACB=90°，AD= $\frac{1}{2}$ AC，BE= $\frac{1}{4}$ AB，猜想∠COD的大小并加以证明．

查看试题解析