安徽省滁州市全椒县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 抛物线的顶点坐标为( )A、 B、 C、 D、2. 反比例函数经过点 , 则下列说法不正确的是( )A、 B、函数图象分布在第一、三象限 C、当时,随的增大而增大 D、当时,随的增大而减小3. 如图,点P在ΔABC的边AC上,下列条件中不能判定的是( )
 A、 B、 C、 D、4. 如图,已知A为反比例函数 ( <0)的图像上一点,过点A作AB⊥ 轴,垂足为B.若△OAB的面积为2,则k的值为( )
A、 B、 C、 D、4. 如图,已知A为反比例函数 ( <0)的图像上一点,过点A作AB⊥ 轴,垂足为B.若△OAB的面积为2,则k的值为( )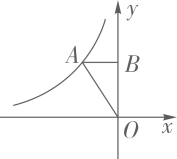 A、2 B、-2 C、4 D、-45. 如图,树AB在路灯O的照射下形成影子AC,已知路灯高m,树影m,树AB与路灯O的水平距离m,点C、A、P在同一水平线上,则树的高度AB长是( )
A、2 B、-2 C、4 D、-45. 如图,树AB在路灯O的照射下形成影子AC,已知路灯高m,树影m,树AB与路灯O的水平距离m,点C、A、P在同一水平线上,则树的高度AB长是( ) A、3m B、2m C、m D、m6. 如图,已知AB和CD是⊙O的两条等弦,OM⊥AB、ON⊥CD,垂足分别为M、N,BA、DC的延长线交于点P,连接OP.下列四个说法:①=;②OM=ON;③PA=PC;④∠BPO=∠DPO;正确的个数是( )
A、3m B、2m C、m D、m6. 如图,已知AB和CD是⊙O的两条等弦,OM⊥AB、ON⊥CD,垂足分别为M、N,BA、DC的延长线交于点P,连接OP.下列四个说法:①=;②OM=ON;③PA=PC;④∠BPO=∠DPO;正确的个数是( ) A、1 B、2 C、3 D、47. 如图,在中,点 , , 分别在边 , , 上,且 , , 若 , 则的值为( )
A、1 B、2 C、3 D、47. 如图,在中,点 , , 分别在边 , , 上,且 , , 若 , 则的值为( )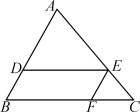 A、 B、 C、 D、8. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )
A、 B、 C、 D、8. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )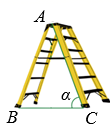 A、 米 B、 米 C、 米 D、 米9. 如图,矩形纸片 , , 点 , 分别在 , 上,把纸片如图沿折叠,点 , 的对应点分别为A' , B' , 连接并延长交线段于点 , 则的值为( )
A、 米 B、 米 C、 米 D、 米9. 如图,矩形纸片 , , 点 , 分别在 , 上,把纸片如图沿折叠,点 , 的对应点分别为A' , B' , 连接并延长交线段于点 , 则的值为( )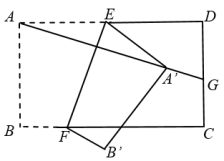 A、 B、 C、 D、10. 在边长为 的正方形 中,对角线 与 相交于点O,P是 上一动点,过P作 ,分别交正方形的两条边于点E,F.设 , 的面积为y,则能反映y与x之间关系的图象为( )
A、 B、 C、 D、10. 在边长为 的正方形 中,对角线 与 相交于点O,P是 上一动点,过P作 ,分别交正方形的两条边于点E,F.设 , 的面积为y,则能反映y与x之间关系的图象为( )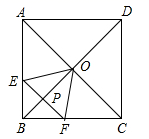 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
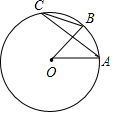
11. 若 ,则 .12. 如图, 、 是 的半径,点C在 上, , ,则 .
 13. 如图,在矩形 中, ,垂足为点 .若 , ,则 的长为.
13. 如图,在矩形 中, ,垂足为点 .若 , ,则 的长为.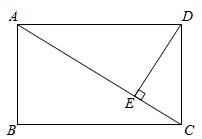 14. 如图(1),四边形ABCD和四边形AEFG都是正方形,将正方形AEFG绕点A旋转,连接BE、CF.
14. 如图(1),四边形ABCD和四边形AEFG都是正方形,将正方形AEFG绕点A旋转,连接BE、CF. (1)、的值为 .(2)、当G、F、C三点共线时,如图(2),若、 , 则 .
(1)、的值为 .(2)、当G、F、C三点共线时,如图(2),若、 , 则 .三、解答题
-
15. 计算:16. 如图,在 和 中, , .
 (1)、求证: ;(2)、若 , ,求 的长.17. 某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为 .
(1)、求证: ;(2)、若 , ,求 的长.17. 某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为 . (1)、求落水点C、D之间的距离;(2)、若需在OD上离O点10米的E处竖立雕塑EF, , 且雕塑的顶部刚好碰到水柱,求雕塑EF的高.18. △ABC在边长为1的正方形网格中如图所示
(1)、求落水点C、D之间的距离;(2)、若需在OD上离O点10米的E处竖立雕塑EF, , 且雕塑的顶部刚好碰到水柱,求雕塑EF的高.18. △ABC在边长为1的正方形网格中如图所示 (1)、以点C为位似中心,作出△ABC的位似图形 , 使ABC与的位似比为1:2,且位于点C的异侧;(2)、作出△ABC绕点C顺时针旋转90°后的图形;19. 如图,一艘快艇A在小岛B的西南方向上相距海里处,另-艘快艇C在快艇A的正东方向上,而小岛B在快艇C的北偏东32°的方向上,已知快艇A的速度是海里/时,若快艇A、C同时出发且同时到达小岛B,求快艇C的速度(精确到个位,参考数据: , , )
(1)、以点C为位似中心,作出△ABC的位似图形 , 使ABC与的位似比为1:2,且位于点C的异侧;(2)、作出△ABC绕点C顺时针旋转90°后的图形;19. 如图,一艘快艇A在小岛B的西南方向上相距海里处,另-艘快艇C在快艇A的正东方向上,而小岛B在快艇C的北偏东32°的方向上,已知快艇A的速度是海里/时,若快艇A、C同时出发且同时到达小岛B,求快艇C的速度(精确到个位,参考数据: , , ) 20. 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
20. 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E. (1)、求证:AE=AB;(2)、若AB=10,BC=6,求CD的长.21. 如图,已知一次函数 与反比例函数 的图象在第一、三象限分别交于 , 两点,连接 , .
(1)、求证:AE=AB;(2)、若AB=10,BC=6,求CD的长.21. 如图,已知一次函数 与反比例函数 的图象在第一、三象限分别交于 , 两点,连接 , .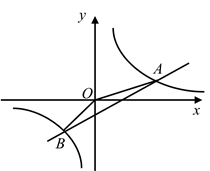 (1)、求一次函数和反比例函数的解析式;(2)、 的面积为;(3)、直接写出 时x的取值范围.
(1)、求一次函数和反比例函数的解析式;(2)、 的面积为;(3)、直接写出 时x的取值范围.