安徽省安庆市怀宁县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-02-28 类型:期末考试
一、单选题
-
1. 下列函数解析式中,一定为二次函数的是( )A、 B、y=ax2+bx+c C、 D、2. 下列各点中,在反比例函数 图象上点的坐标是( )A、 B、 C、 D、3. 抛物线3 的顶点到x轴的距离为( )A、-1 B、-2 C、2 D、34. 2021年7月,占地约2917亩的独秀山公园正式对外全面开放,主办方精心筹建的游乐项目深受广大游客的青睐,其中某两个项目入口之间的距离为155米,在一张比例尺为1:2000的导游图上,它们之间的距离大约相当于( )A、一支粉笔的长度 B、一支钢笔的长度 C、一支铅笔的长度 D、一根筷子的长度5. 下列结论中,不正确的是( )A、若 , 则 B、若 , 则 C、若(b﹣d≠0),则 D、若 , 则a=3,b=46. 下列判断正确的是( )A、对角线相等的四边形是矩形 B、将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似 C、若点是的黄金分割点,且 , 则的长为 D、如果两个相似三角形的面积比为16:9,那么这两个相似三角形的周长比是4:37. 在同一平面直角坐标系中,二次函数y=ax2与一次函数y=bx+c的图象如图所示,则二次函数y=ax2-bx+c的图象可能是( )
 A、
A、 B、
B、 C、
C、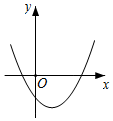 D、
D、 8. 已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法不正确的是( )
8. 已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法不正确的是( )x
…
﹣1
0
1
3
…
y
…
﹣3
1
3
1
…
A、a<0 B、方程ax2+bx+c=﹣2的正根在4与5之间 C、2a+b>0 D、若点(5,y1)、(﹣ , y2)都在函数图象上,则y1<y2二、填空题
-
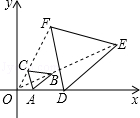
9. 在Rt中, , , 则 .10. 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心,若AB=2,则DE=.
 11. 如图,抛物线y=ax2+c与直线y=mx+n交于两点A(﹣2,p),B(5,q),则不等式ax2+mx+c≤n的解集是 .
11. 如图,抛物线y=ax2+c与直线y=mx+n交于两点A(﹣2,p),B(5,q),则不等式ax2+mx+c≤n的解集是 . 12. 如图,在△ABC中,AC=6,BC=8,D、E分别在CA、CB上,点F在△ABC内.若四边形CDFE是边长为2的正方形,则sin∠FBA= .
12. 如图,在△ABC中,AC=6,BC=8,D、E分别在CA、CB上,点F在△ABC内.若四边形CDFE是边长为2的正方形,则sin∠FBA= .
三、解答题
-
13. 计算:(1)、+- sin60°;(2)、 .14. 已知 , 求的值.15. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).

⑴请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
⑵以点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正切值为 ▲ .
16. 对于二次函数和一次函数 , 把称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E,现有点和抛物线E上的点 , 请完成下列任务; (1)、【尝试】判断点A是否在抛物线E上.(2)、【发现】对于t取任何不为零的实数,抛物线E总过定点,坐标为 .(3)、【应用】以为边作矩形 , 使得其中一个顶点落在y轴上:若抛物线E经过A,B,C,D其中的三点,求出所有符合条件的t的值.
(1)、【尝试】判断点A是否在抛物线E上.(2)、【发现】对于t取任何不为零的实数,抛物线E总过定点,坐标为 .(3)、【应用】以为边作矩形 , 使得其中一个顶点落在y轴上:若抛物线E经过A,B,C,D其中的三点,求出所有符合条件的t的值.