四川省南充市蓬安县2021-2022学年八年级下学期开学考试数学试卷
试卷更新日期：2022-02-28 类型：开学考试
一、选择题（每小题4分，共40分）
-
1. 下列图形是公共设施标志，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列运算正确的是（ ）A、a2·a3＝a6 B、(a2)3＝a5 C、(2a2)3＝8a6 D、a6÷a2＝a33. 在△ABC中，AB≠AC，线段AD，AE，AF分别是△ABC的高，中线，角平分线，则点D，E，F的位置关系为（ ）A、点D总在点E，F之间 B、点E总在点D，F之间 C、点F总在点D，E之间 D、三者的位置关系不确定4. 如图，在△ABC和△DEF中，∠C＝∠F＝90°，添加下列条件，不能判定这两个三角形全等的是（ ）
A、∠A＝∠D，∠B＝∠E B、AC＝DF，AB＝DE C、∠A＝∠D，AB＝DE D、AC＝DF，CB＝FE5. 若等腰三角形的周长为30cm，一边为14cm，则腰长为（ ）A、2cm B、8cm C、8cm或2cm D、14cm或8cm6. 下列各式中，正确的是（ ）A、
B、
C、
D、
7. 在平面直角坐标系中，已知点A (－1，1)， B(－3，2)，点C在坐标轴上，若△ABC是等腰三角形，则满足条件的点C的个数是（ ）A、4个 B、5个 C、7个 D、8个8. ， ， 都有意义，下列等式① ；② ；③ ；④ 中一定不成立的是（ ）A、②④ B、①④ C、①②③④ D、②9. 如图，在△ABC中，AB＝AC，AB的垂直平分线交AB于点E，交BC于点F，连接AF，若∠FAC＝∠B，则∠FAB的度数为（ ）
A、25° B、30° C、35° D、50°10. 如图，等腰Rt△ABC中，AB＝AC ∠BAC＝90°，AD⊥BC于点D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，AM的延长线交BC于点N，连接DM，下列结论：①DF＝DN；②△DMN为等腰三角形；③DM平分∠BMN；④AE＝ EC；⑤AE＝NC. 其中正确结论有（ ）
A、2个 B、3个 C、4个 D、5个二、填空题（每小题4分，共24分）
-
11. 若分式 的值等于0，则x的值为 ．12. 若4·2n＝2，则n＝ ．13. 一个等腰三角形的一边长为4cm，一边长为9cm，则它的周长为 ．14. 如图，在△ABC中，∠A＝40°，∠B＝90°，线段AC的垂直平分线MN与AB交于点D，与AC交于点E，则∠BCD＝.
15. 一般情况下，式子
不成立，但有些数可以使得它成立，例如：a＝－1，b＝2.我们把使得 成立的一对数a、b称之为“相伴数对”，记为(a，b). 若(3，x)是“相伴数对”，则代数式x3－(2x－1)(x＋3)的值为. 16. 如图，点D，E，F分别在等边三角形ABC的三边上，且DE⊥AB，EF⊥BC，FD⊥AC，过点F作FH⊥AB于H，则 的值为.
三、解答题（共86分）
-
17. 化简或计算下列各题(1)、a3·a4·a＋(a2)4＋(－2a4)2；(2)、(2m-1)2-(3m-1)(3m+1)+5m(m-1)；18. 因式分解(1)、9x2y＋6xy＋y．(2)、a4－16．19. 如图，AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D．求∠DBC的度数。
20. 先化简，再求值： ÷( )，其中x＝－1.21. 如图，AD＝BC，AC＝BD，求证：EA＝EB．
22. 如图，△ABC三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．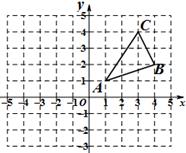
(1)、若△A1B1C1与△ABC关于y轴成轴对称，则△A1B1C1三个顶点的坐标分别为；(2)、△ABC的面积是；(3)、在x轴上作一点P，使PA＋PB的值最小. (保留连线痕迹，不写作法)．23. 某商贩用960元从批发市场购进某种水果销售，由于春节临近，几天后他又用1800元以每千克比第一次高出2元的价格购进这种水果，第二次购进水果的数量是第－次购进数量的1.5倍，设第一次购进水果的数量为x千克.(1)、用含x的式子表示：第二次购进水果为千克，第一次购进水果的单价为元/千克；(2)、该商贩两次购进水果各多少千克？(3)、若商贩将两次购进的水果均按每千克15元的标价进行销售，为了在春节前将水果全部售完，在按标价售出m (100≤m≤200)千克后将余下部分每千克降价a (a为正整数)元全部售出，共获利为1440元，则a的值为(直接写出结果) .24. 如图，△ABC是等边三角形，D、E为AC上两点，且AE＝CD，延长BC至点F，使CF＝CD，连接BD．
(1)、如图1，当D、E两点重合时，求证：BD＝DF；
(2)、延长BD与EF交于点G。①如图2，求证：∠BGE＝60°；
②如图3，连接BE，CG，若∠EBD＝30°，BG＝4，则△BCG的面积为_▲_．
25. 平面直角坐标系中，点A(x，y)，且x2－8x＋16＋
＝0，△ABC是以AB为斜边的等腰直角三角形(点A、B、C逆时针排列).
(1)、直接写出点A的坐标是；(2)、如图1，已知点B(0，n)且0＜n＜4，连接OC. 求四边形ABOC的面积；
(3)、如图2，已知点B(m，n)且0＜m＜4，0＜n＜4，过点A作AD⊥y轴于D，连接OB，M为OB的中点，连接DM、CM. 求证：DM⊥CM.