贵州省凯里学院附中2021-2022学年九年级下学期入学考试数学试卷
试卷更新日期:2022-02-28 类型:开学考试
一、单选题(每小题4分,共40分)
-
1. 2022的相反数是( )A、2022 B、-2022 C、 D、2. 下列运算正确的是( )A、a3 +a3=a6 B、 C、( +2)0=1 D、3. 将直尺和直角三角板按如图方式摆放(∠ACB为直角),已知∠1=30°,则∠2的大小是( )
 A、30° B、45° C、60° D、65°4. 不透明袋子中有除颜色外完全相同的2个黑球和4个白球,从袋中随机摸出3个球,下列事件是必然事件的是( )A、2个白球1个黑球 B、至少有1个白球 C、3个都是白球 D、2个黑球1个白球5. 一个画家有14个边长为1米的正方体,他在地面上把它们摆成如图所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )平方米.
A、30° B、45° C、60° D、65°4. 不透明袋子中有除颜色外完全相同的2个黑球和4个白球,从袋中随机摸出3个球,下列事件是必然事件的是( )A、2个白球1个黑球 B、至少有1个白球 C、3个都是白球 D、2个黑球1个白球5. 一个画家有14个边长为1米的正方体,他在地面上把它们摆成如图所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )平方米. A、19 B、21 C、33 D、366. 若方程 的一个根是-3,则k的值是( )A、-1 B、1 C、2 D、-27. 将抛物线y=x2﹣4x+3向上平移至顶点落在x轴上,如图所示,则两条抛物线、对称轴和y轴围成的图形的面积S(图中阴影部分)是( )
A、19 B、21 C、33 D、366. 若方程 的一个根是-3,则k的值是( )A、-1 B、1 C、2 D、-27. 将抛物线y=x2﹣4x+3向上平移至顶点落在x轴上,如图所示,则两条抛物线、对称轴和y轴围成的图形的面积S(图中阴影部分)是( ) A、1 B、2 C、3 D、48. 如图,AB是⊙O的直径,CD是⊙O的切线,切点为D, CD与AB的延长线交于点C,∠A=30°, ,则 的长度为( )
A、1 B、2 C、3 D、48. 如图,AB是⊙O的直径,CD是⊙O的切线,切点为D, CD与AB的延长线交于点C,∠A=30°, ,则 的长度为( )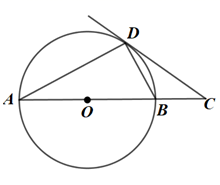 A、4 B、5 C、6 D、79. 在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )A、1个 B、2个 C、3个 D、4个10. 如图,已知四边形 是边长为4的正方形,以对角线 为边作正三角形 ,过点 作 ,交 的延长线于点 ,则 的长是( )
A、4 B、5 C、6 D、79. 在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )A、1个 B、2个 C、3个 D、4个10. 如图,已知四边形 是边长为4的正方形,以对角线 为边作正三角形 ,过点 作 ,交 的延长线于点 ,则 的长是( )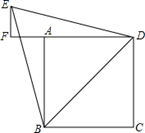 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共30分)
-
11. 2021年2月25日上午,习近平总书记在全国脱贫攻坚总结表彰大会上庄严宣告:历经8年艰苦努力,我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,832个贫困县全部摘帽,12.8万个贫困村全部出列,区域性整体贫困得到解决.用科学记数法表示9899万人为人.12. 把多项式 分解因式的结果是.13. 某校对甲、乙两名跳高运动员的近期跳高成绩进行统计分析,结果如下: , , , ,则这两名运动员中的的成绩更稳定.14. 如图,菱形ABCD中,∠ABC=130°,DE⊥AB于点E,则∠BDE=°
 15. 在平面直角坐标系中,点 , ,以原点O为位似中心,把 扩大为原来2倍,则点B的对应点 的坐标是.
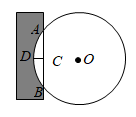
15. 在平面直角坐标系中,点 , ,以原点O为位似中心,把 扩大为原来2倍,则点B的对应点 的坐标是. 16. 不等式组 的解集为.17. 《九章算术》被尊为古代数学“群经之首”,其卷九勾股篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深 等于1寸,锯道 长1尺,问圆形木材的直径是多少?(1尺=10寸)
16. 不等式组 的解集为.17. 《九章算术》被尊为古代数学“群经之首”,其卷九勾股篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深 等于1寸,锯道 长1尺,问圆形木材的直径是多少?(1尺=10寸)答:圆形木材的直径寸;
 18. 圆锥的底面半径是1,侧面积是3π,则这个圆锥的侧面展开图的圆心角为 .19. 已知如图,在 ABO中,∠ABO=90°,∠AOB=30°,A在x轴上,B在反比例函数 上,则 ABO的面积是
18. 圆锥的底面半径是1,侧面积是3π,则这个圆锥的侧面展开图的圆心角为 .19. 已知如图,在 ABO中,∠ABO=90°,∠AOB=30°,A在x轴上,B在反比例函数 上,则 ABO的面积是 20. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),该抛物线的部分图象如图所示,下列结论:①4ac<b2; ②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③3a+c>0; ④当x<0时,y随x增大而减小;⑤点P(m , n)是抛物线上任意一点,则m(am+b)≤a+b , 其中正确的结论是 .(填写序号)
20. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),该抛物线的部分图象如图所示,下列结论:①4ac<b2; ②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③3a+c>0; ④当x<0时,y随x增大而减小;⑤点P(m , n)是抛物线上任意一点,则m(am+b)≤a+b , 其中正确的结论是 .(填写序号)
三、解答题(共80分)
-
21.(1)、计算:(2)、先化简 ,再从-1、0、1中选择合适的x值代入求值.22. 张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别
频数分组
频率
A
x<6000
0.1
B
6000≤x<7000
0.5
C
7000≤x<8000
m
D
x≥8000
n
合计
1

根据信息解答下列问题:
(1)、填空:m= , n= ;并补全条形统计图;(2)、这20名朋友一天行走步数的中位数落在组;(填组别)(3)、张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.23. 如图,AB为⊙O的直径,BC是⊙O的一条弦,点D在⊙O上,BD平分∠ABC,过点D作EF⊥BC,分别交BA、BC的延长线于点E、F. (1)、求证:EF为⊙O的切线;(2)、若BD=4 ,tan∠FDB=2,求AE的长.24. 在全国人民的努力下,中国新冠疫情得到了有效控制,但是仍存在小范围反弹的危险,所以我们仍要严加防控,注意个人防护.某药店销售A 、B两种类型的囗罩,已知销售800包A型口罩和450包B型口罩的利润为2100元,销售400包A型口罩和600包B型口罩的利润为1800元,(1)、求每包A型口罩和B型口罩的利润.(2)、该药店计划一次购进两种型号的口罩2000包,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x包,这2000包口罩的利润为y元.
(1)、求证:EF为⊙O的切线;(2)、若BD=4 ,tan∠FDB=2,求AE的长.24. 在全国人民的努力下,中国新冠疫情得到了有效控制,但是仍存在小范围反弹的危险,所以我们仍要严加防控,注意个人防护.某药店销售A 、B两种类型的囗罩,已知销售800包A型口罩和450包B型口罩的利润为2100元,销售400包A型口罩和600包B型口罩的利润为1800元,(1)、求每包A型口罩和B型口罩的利润.(2)、该药店计划一次购进两种型号的口罩2000包,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x包,这2000包口罩的利润为y元.①求y关于x的函数关系式
②该药店购进A、B型口罩各多少包才能使销售总利润最大?
25. 阅读下面材料,并解答其后的问题:定义:两组邻边分别相等的四边形叫做筝形.
如图1,四边形ABCD中,若AD=AB,CD=CB,则四边形ABCD是筝形.

类比研究:
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对平行四边形的性质进行研究,请根据示例图形,完成下表:
四边形
示例图形
对称性
边
角
对角线
平行
四边形

是中心对称图形
两组对边分别平行,两组对边分别相等.
两组对角
分别相等.
对角线互相平分.
筝形

①
两组邻边分别相等
有一组对角相等
②
(1)、表格中①、②分别填写的内容是:①;
②.
(2)、演绎论证:证明筝形有关对角线的性质.如图2,已知:在筝形ABCD中,AD=AB,BC=DC,AC、BD是对角线.
求证: ▲ .
证明:
(3)、运用:如图3,已知筝形ABCD中,AD=AB=4,CD=CB,∠A=90°,∠C=60°,求筝形ABCD的面积.26. 如图,在直角坐标系中,直线 与 轴、 轴的交点分别为 、 ,以 为对称轴的抛物线 与 轴分别交于点 、 .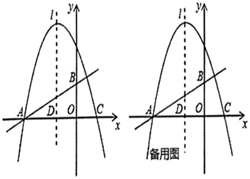 (1)、求抛物线的解析式;(2)、若点 是第二象限内抛物线上的动点,其横坐标为 .设抛物线的对称轴 与 轴交于点 ,连接 ,交 于 ,求出当以 、 、 为顶点的三角形与 相似时点 的坐标;(3)、点 是对称轴上任意一点,在抛物线上是否存在点 ,使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、若点 是第二象限内抛物线上的动点,其横坐标为 .设抛物线的对称轴 与 轴交于点 ,连接 ,交 于 ,求出当以 、 、 为顶点的三角形与 相似时点 的坐标;(3)、点 是对称轴上任意一点,在抛物线上是否存在点 ,使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,说明理由.