2021-2022学年浙教版数学九下第三章 投影与三视图 单元检测卷
试卷更新日期:2022-02-27 类型:单元试卷
一、单选题
-
1. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
 B、
B、 C、
C、 D、
D、 2. 深圳湾“春笋”大楼的顶部如图所示,则该几何体的主视图是( )
2. 深圳湾“春笋”大楼的顶部如图所示,则该几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 在如图所示的几何体中,从不同方向看得到的平面图形中有长方形的是( )
3. 在如图所示的几何体中,从不同方向看得到的平面图形中有长方形的是( )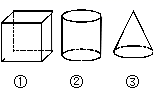 A、① B、② C、①② D、①②③4. 下面四个立体图形中,从正面看是三角形的是( )A、
A、① B、② C、①② D、①②③4. 下面四个立体图形中,从正面看是三角形的是( )A、 B、
B、 C、
C、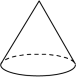 D、
D、 5. 某几何体的三视图如图所示,这个几何体是( )
5. 某几何体的三视图如图所示,这个几何体是( ) A、三棱柱 B、球体 C、圆锥体 D、圆柱体6. 如图是某个几何体的展开图,该几何体是( )
A、三棱柱 B、球体 C、圆锥体 D、圆柱体6. 如图是某个几何体的展开图,该几何体是( )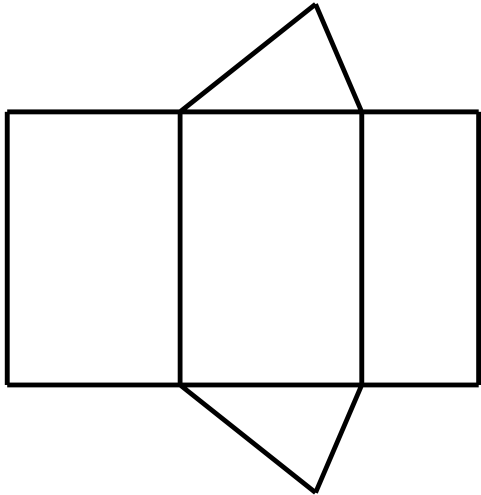 A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱7. 如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分是落在地面的CE,一部分是落在墙EF上的EH.若量得米,米,则立柱CD的高为( ).
A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱7. 如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分是落在地面的CE,一部分是落在墙EF上的EH.若量得米,米,则立柱CD的高为( ).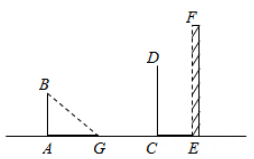 A、2.5m B、2.7m C、3m D、3.6m8. 如图是由4个相同的小长方体组成的立体图形和它的主视图,则它的俯视图为( )
A、2.5m B、2.7m C、3m D、3.6m8. 如图是由4个相同的小长方体组成的立体图形和它的主视图,则它的俯视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( )
9. 如图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、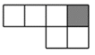 10. 如图,图形不是下边哪个图形的展开图( )
10. 如图,图形不是下边哪个图形的展开图( )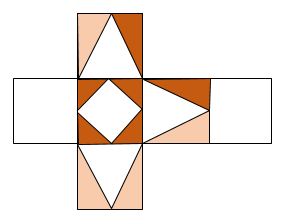 A、
A、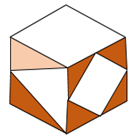 B、
B、 C、
C、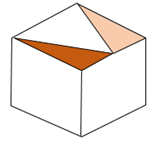 D、
D、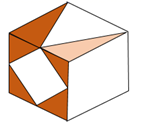
二、填空题
-
11. 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是正方体的平面展开图,若图中的“锦”表示正方体的右面,则“”表示正方体的左面
 12. 观察右边立体图得到它的主视图、左视图和俯视图,请写在对应图的下边.
12. 观察右边立体图得到它的主视图、左视图和俯视图,请写在对应图的下边.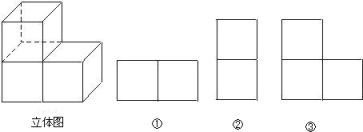
① , ② , ③ .
13. 如图,从一块半径是1m的圆形铁皮上剪出一个圆心角为90°的扇形围成一个圆锥,则这个圆锥的底面半径是m.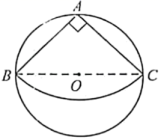 14. 一个几何体由若干个大小相同的小立方块搭成,从左面和上面看到的平面图形如图所示,则搭成这个几何体的小立方块的个数为 .
14. 一个几何体由若干个大小相同的小立方块搭成,从左面和上面看到的平面图形如图所示,则搭成这个几何体的小立方块的个数为 .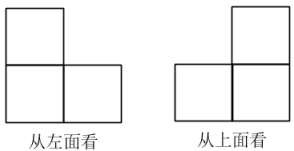 15. 平行于墙面的三角尺在灯泡O的照射下在墙上形成的影子如图所示.若 , ,则三角尺与它在墙上影子的周长比是.
15. 平行于墙面的三角尺在灯泡O的照射下在墙上形成的影子如图所示.若 , ,则三角尺与它在墙上影子的周长比是. 16. 用小立方块搭成的几何体;从正面看到的图形和从上面看到的图形如下图,问搭成这样的几何体最多需要个小立方块,最少需要个小立方块.
16. 用小立方块搭成的几何体;从正面看到的图形和从上面看到的图形如下图,问搭成这样的几何体最多需要个小立方块,最少需要个小立方块.
三、解答题
-
17. 小明同学要测量学校旗杆AB的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为0.8米,同时测量旗杆AB的影长时,由于影子不全落在地面上,他测得地面上的影长BC为6米,留在墙上的影高CD为3米,请利用以上信息,求旗杆AB的高度.
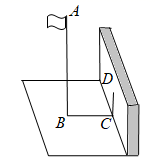 18. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
18. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,求该圆锥的高h的长. 19. 【综合与实践】现实生活中,人们可以借助光源来测量物体的高度.已知榕树CD,FG和灯柱AB如图①所示,在灯柱AB上有一盏路灯P,榕树和灯柱的底端在同一水平线上,两棵榕树在路灯下都有影子,只要测量出其中一些数据,则可求出所需要的数据,具体操作步骤如下:
19. 【综合与实践】现实生活中,人们可以借助光源来测量物体的高度.已知榕树CD,FG和灯柱AB如图①所示,在灯柱AB上有一盏路灯P,榕树和灯柱的底端在同一水平线上,两棵榕树在路灯下都有影子,只要测量出其中一些数据,则可求出所需要的数据,具体操作步骤如下: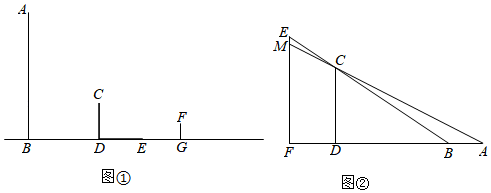
①根据光源确定榕树在地面上的影子;
②测量出相关数据,如高度,影长等;
③利用相似三角形的相关知识,可求出所需要的数据.
根据上述内容,解答下列问题:
(1)、已知榕树CD在路灯下的影子为DE,请画出榕树FG在路灯下的影子GH;(2)、如图①,若榕树CD的高度为3.6米,其离路灯的距离BD为6米,两棵榕树的影长DE,GH均为4米,两棵树之间的距离DG为6米,求榕树FG的高度;(3)、无论太阳光还是点光源,其本质与视线问题相同.日常生活中我们也可以直接利用视线解决问题.如图②,建筑物CD高为50米,建筑物MF上有一个广告牌EM,合计总高度EF为70米,两座建筑物之间的直线距离FD为30米.一个观测者(身高不计)先站在A处观测,发现能看见广告牌EM的底端M处,观测者沿着直线AF向前走了5米到B处观测,发现刚好看到广告牌EM的顶端E处.则广告牌EM的高度为 米.20. 如图是由10个大小相同的小立方体搭建的几何体,其中每个小立方体的棱长为1厘米. (1)、请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图;(2)、若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加个小正方体(直接填空).21. 如图所示,D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连结AB,AC,AD,E为AD上一点,连结BE,CE.
(1)、请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图;(2)、若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加个小正方体(直接填空).21. 如图所示,D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连结AB,AC,AD,E为AD上一点,连结BE,CE.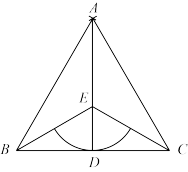 (1)、求证:BE = CE.(2)、以点E为圆心作与BC相切,分别交BE,CE于点F,G.若BC = 4,∠EBD = 30°,求扇形FEG的面积(3)、若用扇形FEG围成一个圆锥的侧面,求这个圆锥的底面圆的半径.22. 如图是一个长方体纸盒的平面展开图,纸盒中相对两个面上的数互为相反数.
(1)、求证:BE = CE.(2)、以点E为圆心作与BC相切,分别交BE,CE于点F,G.若BC = 4,∠EBD = 30°,求扇形FEG的面积(3)、若用扇形FEG围成一个圆锥的侧面,求这个圆锥的底面圆的半径.22. 如图是一个长方体纸盒的平面展开图,纸盒中相对两个面上的数互为相反数.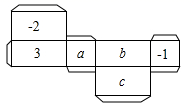 (1)、填空: , , ;(2)、先化简,再求值: .23. 几何体的三视图相互关联.已知直三棱柱的三视图如图,在 中, , , .
(1)、填空: , , ;(2)、先化简,再求值: .23. 几何体的三视图相互关联.已知直三棱柱的三视图如图,在 中, , , . (1)、求 及 的长;(2)、若主视图与左视图两矩形相似,求 的长;(3)、在(2)的情况下,求直三棱柱的表面积.24. 在一次青少年模型大赛中,小高和小刘各制作了一个模型,小高制作的是棱长为acm的正方体模型,小刘制作的是棱长为acm的正方体右上角割去一个长为3cm,宽为2cm,高为1cm的长方体模型(如图2)
(1)、求 及 的长;(2)、若主视图与左视图两矩形相似,求 的长;(3)、在(2)的情况下,求直三棱柱的表面积.24. 在一次青少年模型大赛中,小高和小刘各制作了一个模型,小高制作的是棱长为acm的正方体模型,小刘制作的是棱长为acm的正方体右上角割去一个长为3cm,宽为2cm,高为1cm的长方体模型(如图2) (1)、用含a的代数式表示,小高制作的模型的各棱长度之和是;(2)、若小高的模型各棱长之和是小刘的模型各棱长之和的 ,求a的值;(3)、在(2)的条件下,
(1)、用含a的代数式表示,小高制作的模型的各棱长度之和是;(2)、若小高的模型各棱长之和是小刘的模型各棱长之和的 ,求a的值;(3)、在(2)的条件下,①图3是小刘制作的模型中正方体六个面的展开图,图中缺失的有一部分已经很用阴影表示,请你用阴影表示出其余缺失部分,并标出边的长度.
②如果把小刘的模型中正方体的六个面展开,则展开图的周长是 ▲ cm;请你在图方格中画出小刘的模型中正方体六个面的展开图周长最大时的图形.
