2021-2022学年浙教版数学九下第一章单元检测卷
试卷更新日期:2022-02-27 类型:单元试卷
一、单选题
-
1. 在Rt△ABC中,∠C=90°,那么等于( )A、 B、 C、 D、2. 已知在RtABC中,∠C=90°,AB=c,AC=b,那么下列结论一定成立的是( )A、b=ctanA B、b=ccotA C、b=csinA D、b=ccosA3. 在中, , , 那么的长是( )A、 B、 C、 D、4. 如图,在△ABC中,∠C=90°,AB=5,AC=4,则tanB的值是( )
 A、 B、 C、 D、5. 在中, , , , 那么下列各式中正确的是( )A、 B、 C、 D、6. 如图,有一个弓形的暗礁区,弓形所含的圆周角 , 船在航行时,为保证不进入暗礁区,则船到两个灯塔A,B的张角应满足的条件是( )
A、 B、 C、 D、5. 在中, , , , 那么下列各式中正确的是( )A、 B、 C、 D、6. 如图,有一个弓形的暗礁区,弓形所含的圆周角 , 船在航行时,为保证不进入暗礁区,则船到两个灯塔A,B的张角应满足的条件是( ) A、 B、 C、 D、7. 如图,梯子(长度不变)跟地面所成的锐角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A、 B、 C、 D、7. 如图,梯子(长度不变)跟地面所成的锐角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )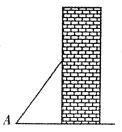 A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关8. 如图,△ABC是锐角三角形,sinC= ,则sin A的取值范围是( )
A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关8. 如图,△ABC是锐角三角形,sinC= ,则sin A的取值范围是( )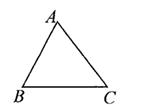 A、0<sinA< B、 <SinA<1 C、 <sinA< D、 <sinA<19. 如图是一段索道的示意图. 若 米, , 则洗车从 点到 点上升的高度 的长为( )
A、0<sinA< B、 <SinA<1 C、 <sinA< D、 <sinA<19. 如图是一段索道的示意图. 若 米, , 则洗车从 点到 点上升的高度 的长为( ) A、 米 B、 米 C、 米 D、 米10. 在 Rt 中, , 如果 , 那么等于( )A、 B、 C、 D、
A、 米 B、 米 C、 米 D、 米10. 在 Rt 中, , 如果 , 那么等于( )A、 B、 C、 D、二、填空题
-
11. 先用计算器求:cos20°≈ , cos40°≈ , cos60°≈ , cos80°≈ , 再按从大到小的顺序用“>”把cos20°,cos40°,cos60°,cos80°连接起来: . 归纳:余弦值,角大值 .12. 如图, 将直径 的半圆 , 绕端点 逆时针旋转, 当圆弧与直径交点 满足 时, 的值为.
 13. 如图,在Rt△ABC中,∠C=90°,∠A=30°,分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧交于M,N两点,连结MN分别交 AB,AC于点E,D,若 AD=8,则AB的长为.
13. 如图,在Rt△ABC中,∠C=90°,∠A=30°,分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧交于M,N两点,连结MN分别交 AB,AC于点E,D,若 AD=8,则AB的长为.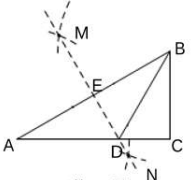 14. 比较大小:sin80°tan50°(填“>”或“<”).15. 如图,在中, , , 点是上一点,点是延长线上一点,已知 , , 则的长为 .
14. 比较大小:sin80°tan50°(填“>”或“<”).15. 如图,在中, , , 点是上一点,点是延长线上一点,已知 , , 则的长为 . 16. 如图,飞机在目标的正上方处,飞行员测得地面目标的俯角 , 如果地面目标、之间的距离为千米,那么飞机离地面的高度等于千米.(结果保留根号)
16. 如图,飞机在目标的正上方处,飞行员测得地面目标的俯角 , 如果地面目标、之间的距离为千米,那么飞机离地面的高度等于千米.(结果保留根号)
三、解答题
-
17. 如图,为了测量建筑物的高度,先从与建筑物的底部点水平相距100米的点处出发,沿斜坡行走至坡顶处,斜坡的坡度 , 坡顶到的距离米,在点处测得建筑物顶端点的仰角为 , 点在同一平面内,根据测量数据,请计算建筑物的高度(结果精确到1米).(参考数据:)
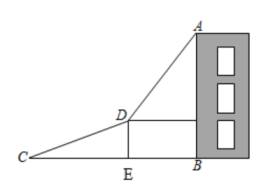 18. 某货站沿斜坡AB将货物传送到平台BC.一个正方体木箱沿着斜坡移动,当木箱的底部到达点B时的平面示意图如图所示.已知斜坡AB的坡度为1:2.4,点B到地面的距离BE=1.5米,正方体木箱的棱长BF=0.65米,求点F到地面的距离.
18. 某货站沿斜坡AB将货物传送到平台BC.一个正方体木箱沿着斜坡移动,当木箱的底部到达点B时的平面示意图如图所示.已知斜坡AB的坡度为1:2.4,点B到地面的距离BE=1.5米,正方体木箱的棱长BF=0.65米,求点F到地面的距离.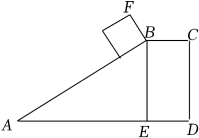 19. 如图,某校的实验楼对面是一幢教学楼,小张在实验楼的窗口C(ACBD)处测得教学楼顶部D的仰角为27°,教学楼底部B的俯角为13°,量得实验楼与教学楼之间的距离AB=20米.求教学楼BD(BD⊥AB)的高度.(精确到0.1米)(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
19. 如图,某校的实验楼对面是一幢教学楼,小张在实验楼的窗口C(ACBD)处测得教学楼顶部D的仰角为27°,教学楼底部B的俯角为13°,量得实验楼与教学楼之间的距离AB=20米.求教学楼BD(BD⊥AB)的高度.(精确到0.1米)(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,sin27°≈0.45,cos27°≈0.89,tan27°≈0.51) 20. 如图为一种翻盖式圆柱形茶杯,底面直径为15cm,高为20cm.
20. 如图为一种翻盖式圆柱形茶杯,底面直径为15cm,高为20cm.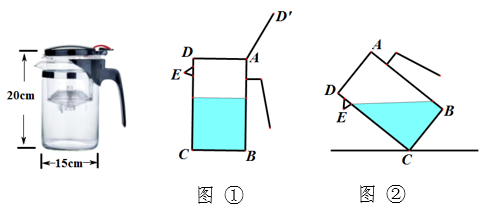 (1)、如图①,小明通过按压点A打开杯盖AD注入热水(点D,D’为对应点).若∠DAD’=120°,求点D的运动路径长.(2)、如图②,将茶杯支在桌子上,当杯底倾斜到与桌面呈53°时,恰好将热水倒出,求此时杯子最高点A距离桌面的距离.(参考数据sin53°≈0.8,cos53°≈0.6)21. 如图,已知AB是⊙O的直径,AB=6,sinC= .
(1)、如图①,小明通过按压点A打开杯盖AD注入热水(点D,D’为对应点).若∠DAD’=120°,求点D的运动路径长.(2)、如图②,将茶杯支在桌子上,当杯底倾斜到与桌面呈53°时,恰好将热水倒出,求此时杯子最高点A距离桌面的距离.(参考数据sin53°≈0.8,cos53°≈0.6)21. 如图,已知AB是⊙O的直径,AB=6,sinC= . (1)、求弦AD的长.(2)、过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.求DF的长.22. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量翡翠湖某处东西岸边 , 两点之间的距离.如图所示,小星站在湖边的处遥控无人机,无人机在处距离地面的飞行高度是 , 此时从无人机测得岸边处的俯角为 , 他抬头仰视无人机时,仰角为 , 若小星的身高 , (点 , , , 在同一平面内).
(1)、求弦AD的长.(2)、过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.求DF的长.22. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量翡翠湖某处东西岸边 , 两点之间的距离.如图所示,小星站在湖边的处遥控无人机,无人机在处距离地面的飞行高度是 , 此时从无人机测得岸边处的俯角为 , 他抬头仰视无人机时,仰角为 , 若小星的身高 , (点 , , , 在同一平面内). (1)、求仰角的正弦值;(2)、求 , 两点之间的距离(结果精确到).( , , , , , )23. 如图,已知在中, , 垂足为点 , 点是边的中点.
(1)、求仰角的正弦值;(2)、求 , 两点之间的距离(结果精确到).( , , , , , )23. 如图,已知在中, , 垂足为点 , 点是边的中点. (1)、求边的长;(2)、求的正弦值.24. 如图1,在平面直角坐标系中, 为坐标原点,直线 与 轴交于点 ,与 轴交于点 ,直线 交 于点 ,点 的横坐标为 .
(1)、求边的长;(2)、求的正弦值.24. 如图1,在平面直角坐标系中, 为坐标原点,直线 与 轴交于点 ,与 轴交于点 ,直线 交 于点 ,点 的横坐标为 . (1)、求直线 的解析式;(2)、如图2,点 在第二象限,直线 上一点,连接 ,过点 作 的垂线 ,在 上截取线段 , ,点 在第一象限,过点 作 轴于点 ,设点 的横坐标为 ,线段 的长为 ,求 与 之间的函数关系式(不要求写自变量 的取值范围);(3)、如图3,在(2)的条件下,过点 作 交 的延长线于点 ,连接 ,点 为 中点,连接 并延长 交 轴于点 ,连接 、 ,当 时,求点 的坐标.
(1)、求直线 的解析式;(2)、如图2,点 在第二象限,直线 上一点,连接 ,过点 作 的垂线 ,在 上截取线段 , ,点 在第一象限,过点 作 轴于点 ,设点 的横坐标为 ,线段 的长为 ,求 与 之间的函数关系式(不要求写自变量 的取值范围);(3)、如图3,在(2)的条件下,过点 作 交 的延长线于点 ,连接 ,点 为 中点,连接 并延长 交 轴于点 ,连接 、 ,当 时,求点 的坐标.