新疆昌吉教育体系2022届高三上学期理数第四次诊断测试试卷
试卷更新日期:2022-02-25 类型:月考试卷
一、单选题
-
1. 设复数在复平面内对应的点为 , 则的虚部为( )A、 B、-1 C、1 D、32. 设p: , : , 则p是q成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 已知 , 满足约束条件 ,则 的最大值为( )A、0 B、2 C、4 D、64. 函数 的图像大致是( )A、
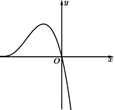 B、
B、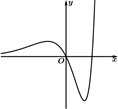 C、
C、 D、
D、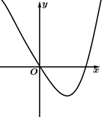 5. 若向量 ,则 与 的夹角余弦值为( )A、 B、 C、 D、6. 已知数列 的前 项和为 ,若 ,则 =( )A、 B、 C、 D、7. 在 中,内角A,B,C所对的边分别为a,b,c,已知(a+b-c)(a+b+c)=3ab,且c=4,则 面积的最大值为( )A、8 B、4 C、2 D、8. 圆 关于直线 对称的圆的方程为( )A、 B、 C、 D、9. 已知函数 为 上偶函数,且 在 上的单调递增,若 ,则满足 的 的取值范围是( )A、 B、 C、 D、10. 已知函数f(x)=x(lnx-ax)有两个极值点,则实数a的取值范围是( )A、(-∞,0) B、 C、(0,1) D、(0,+∞)11. 函数 的图像与直线 在区间 上恰有三个交点,其横坐标分别为 ,则 的取值范围为( )A、 B、 C、 D、12. 已知正方形 的内切圆的半径为1,点M是圆上的一动点,则 的取值范围是( )A、 B、 C、 D、
5. 若向量 ,则 与 的夹角余弦值为( )A、 B、 C、 D、6. 已知数列 的前 项和为 ,若 ,则 =( )A、 B、 C、 D、7. 在 中,内角A,B,C所对的边分别为a,b,c,已知(a+b-c)(a+b+c)=3ab,且c=4,则 面积的最大值为( )A、8 B、4 C、2 D、8. 圆 关于直线 对称的圆的方程为( )A、 B、 C、 D、9. 已知函数 为 上偶函数,且 在 上的单调递增,若 ,则满足 的 的取值范围是( )A、 B、 C、 D、10. 已知函数f(x)=x(lnx-ax)有两个极值点,则实数a的取值范围是( )A、(-∞,0) B、 C、(0,1) D、(0,+∞)11. 函数 的图像与直线 在区间 上恰有三个交点,其横坐标分别为 ,则 的取值范围为( )A、 B、 C、 D、12. 已知正方形 的内切圆的半径为1,点M是圆上的一动点,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 若 , , , 则的最小值为 .14. 已知三棱锥 中, 底面 , , ,且该三棱锥所有顶点都在球O的球面上,则球O的表面积为.15. 已知直线l的方程为 ,其中 求出当m变化时,点 到直线l的距离的最大值为 .16. 设锐角 三个内角 , , 所对应的边分别为 , , ,若 , , ,则 .
三、解答题
-
17. 的内角A,B,C的对边分别为a,b,c,且满足(1)、求角A的大小;(2)、求 的取值范围.18. 已知 为坐标原点, , ,若 .(1)、求函数 的最小正周期;(2)、当 时,求函数 的值域.19. 已知数列是等差数列,数列是各项均为正数的等比数列,且.(1)、求数列 , 的通项公式;(2)、求数列的前n项和.20. 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=B1C1=1.
 (1)、求证:平面AB1C⊥平面BB1D;(2)、求二面角A1-BD-C1的余弦值.
(1)、求证:平面AB1C⊥平面BB1D;(2)、求二面角A1-BD-C1的余弦值.
