湖南省名校联合体2021-2022学年高三上学期数学12月联考试卷
试卷更新日期:2022-02-25 类型:月考试卷
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 若复数 (i为虚数单位)则 ( )A、 B、 C、 D、3. 已知向量 ,若 ,则 ( )A、 B、 C、 D、54. 已知 ,则 ( )A、-1 B、1 C、-5 D、55. 1859年,英国作家约翰·泰勒(John Taylor,1781-1846)在其《大金字塔》一书中提出:古埃及人在建造胡夫金字塔时利用了黄金数( ).泰勒还引用了古希腊历史学家希罗多德的记载:胡夫金字塔的形状为正四棱锥,每一个侧面的面积都等于金字塔高的平方.如图,已知金字塔型正四棱锥 的底面边长约为656英尺,顶点P在底面上的投影为底面的中心O,H为线段BC的中点,根据以上信息, 的长度(单位:英尺)约为( )
 A、302.7 B、405.4 C、530.7 D、1061.46. 函数 的图象大致为( )A、
A、302.7 B、405.4 C、530.7 D、1061.46. 函数 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 7. 已知抛物线上一点到焦点的距离为3,准线为l,若l与双曲线的两条渐近线所围成的三角形面积为 , 则双曲线C的离心率为( )A、3 B、 C、 D、8. 在等比数列 中, ,则 ( )A、-6 B、 C、 D、2
7. 已知抛物线上一点到焦点的距离为3,准线为l,若l与双曲线的两条渐近线所围成的三角形面积为 , 则双曲线C的离心率为( )A、3 B、 C、 D、8. 在等比数列 中, ,则 ( )A、-6 B、 C、 D、2二、多选题
-
9. 已知二项式 的展开式中共有8项,则下列说法正确的有( )A、所有项的二项式系数和为128 B、所有项的系数和为1 C、二项式系数最大的项为第5项 D、有理项共3项10. 已知函数 ,将函数 的图象上所有点的横坐标伸长为原来的3倍,纵坐标不变,再向左平移 个单位长度,向上平移2个单位长度,得到函数 的图象,则以下结论正确的是( )A、 的最大值为1 B、函数 的单调递增区间为 C、 是函数 的一条对称轴 D、 是函数 的一个对称中心11. 已知圆 和直线 ,则( )A、直线l与圆C的位置关系无法判定 B、当 时,圆C上的点到直线l的最远距离为 C、当圆C上有且仅有3个点到直线l的距离等于1时, D、如果直线l与圆C相交于M、N两点,则MN的中点的轨迹是一个圆12. 已知图1中,正方形 的边长为 ,A、B、C、D是各边的中点,分别沿着 、 、 、 把 、 、 、 向上折起,使得每个三角形所在的平面都与平面 垂直,再顺次连接 ,得到一个如图2所示的多面体,则( )
 A、平面 平面 B、直线 与直线 所成的角为 C、多面体 的体积为 D、直线 与平面 所成角的正切值为
A、平面 平面 B、直线 与直线 所成的角为 C、多面体 的体积为 D、直线 与平面 所成角的正切值为三、填空题
-
13. 已知 为奇函数,当 时, ,则 .14. 从下图12个点中任取三个点则所取的三个点能构成三角形的概率为 .
 15. 某同学在参加魔方实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为 的正方体的六个面所截后剩余的部分(球心与正方体的中心重合),若其中一个截面圆的周长为 ,则该球的半径是 .
15. 某同学在参加魔方实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为 的正方体的六个面所截后剩余的部分(球心与正方体的中心重合),若其中一个截面圆的周长为 ,则该球的半径是 . 16. 已知(1)、函数 的零点个数为个;(2)、若 的图象与x轴有3个不同的交点,则实数a的取值范围为 .
16. 已知(1)、函数 的零点个数为个;(2)、若 的图象与x轴有3个不同的交点,则实数a的取值范围为 .四、解答题
-
17. 已知 是等差数列,其前 项和为 .若 .(1)、求 的通项公式;(2)、设 ,数列 的前 项和为 ,求 .18. 已知 的内角A,B,C的对边分别为a,b,c,且 (其中S为 的面积).(1)、求角B的大小;(2)、若 为锐角三角形,且 ,求a的取值范围.19. 某电视台招聘节目主持人,甲、乙两人同时应聘.应聘者需进行笔试和面试,笔试分为三个环节,每个环节都必须参与,甲笔试部分每个环节通过的概率均为 ,乙笔试部分每环节通过的概率依次为 ,笔试三个环节至少通过两个才能够参加面试,否则直接淘汰;面试分为两个环节,每个环节都必须参与,甲面试部分每个环节通过的概率依次为 , ,乙面试部分每个环节通过的概率依次为 .若面试部分的两个环节都通过,则可以成为该电视台的节目主持人.甲、乙两人通过各个环节相互独立.(1)、求乙能参与面试的概率;(2)、记甲本次应聘通过的环节数为X,求X的分布列以及数学期望.20. 如图,已知四棱台 的上、下底面分别是边长为2和4的正方形, ,且 底面 ,点 分别在棱 、 上·
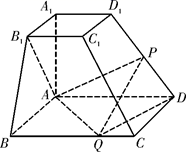 (1)、若P是 的中点,证明: ;(2)、若 平面 ,二面角 的余弦值为 ,求四面体 的体积.
(1)、若P是 的中点,证明: ;(2)、若 平面 ,二面角 的余弦值为 ,求四面体 的体积.