山东省济南市莱芜区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-25 类型:期末考试
一、单选题
-
1. “疫情就是命令,防控就是责任”,面对疫情,其中图案是轴对称图形的是( )A、
 B、
B、 C、
C、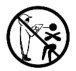 D、
D、 2. 已知三角形的三边长分别为2、x、8,则x的值可能是( )A、4 B、6 C、9 D、103. 若点P(-2,1)关于y轴的对称点为Q(a,b),则点Q的坐标为( )A、(2,1) B、(-2,-1) C、(2,-1) D、(-2,1)4. 在平面直角坐标系中,下列各点中到x轴的距离是4,且在第四象限的是( )A、(4,﹣5) B、(﹣4,5) C、(﹣5,4) D、(5,﹣4)5. 一个正比例函数的图象经过点A(﹣2,3)点B(a,﹣3),则a的值是( )A、2 B、﹣2 C、 D、﹣6. 盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,使其窗框不变形如图所示 , 这样做的数学依据是( )
2. 已知三角形的三边长分别为2、x、8,则x的值可能是( )A、4 B、6 C、9 D、103. 若点P(-2,1)关于y轴的对称点为Q(a,b),则点Q的坐标为( )A、(2,1) B、(-2,-1) C、(2,-1) D、(-2,1)4. 在平面直角坐标系中,下列各点中到x轴的距离是4,且在第四象限的是( )A、(4,﹣5) B、(﹣4,5) C、(﹣5,4) D、(5,﹣4)5. 一个正比例函数的图象经过点A(﹣2,3)点B(a,﹣3),则a的值是( )A、2 B、﹣2 C、 D、﹣6. 盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,使其窗框不变形如图所示 , 这样做的数学依据是( )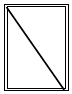 A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短7. 如图,ABC中,∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC,如果BC=8cm,则DEC的周长是( )
A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短7. 如图,ABC中,∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC,如果BC=8cm,则DEC的周长是( ) A、6cm B、8cm C、9cm D、10cm8. 如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为4和6,则正方形B的面积为( )
A、6cm B、8cm C、9cm D、10cm8. 如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为4和6,则正方形B的面积为( )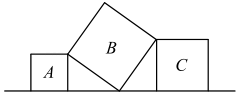 A、26 B、49 C、52 D、649. 已知k<0,则一次函数y=-kx+k的图象大致是( )A、
A、26 B、49 C、52 D、649. 已知k<0,则一次函数y=-kx+k的图象大致是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,ABC和ECD都是等腰直角三角形,∠ACB=∠DCE=90°,ABC的顶点A在ECD的斜边DE上.下列结论不正确的是( )
10. 如图,ABC和ECD都是等腰直角三角形,∠ACB=∠DCE=90°,ABC的顶点A在ECD的斜边DE上.下列结论不正确的是( )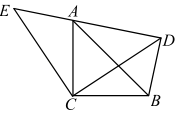 A、ACE≌BCD B、∠DAB=45° C、AD+DB=DE D、ABD是直角三角形11. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行3600米,先到终点的人原地休息.已知甲先出发6分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,以下结论:①甲步行的速度为60米/分;②乙走完全程用了48分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有1200米.其中正确的结论有( )
A、ACE≌BCD B、∠DAB=45° C、AD+DB=DE D、ABD是直角三角形11. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行3600米,先到终点的人原地休息.已知甲先出发6分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,以下结论:①甲步行的速度为60米/分;②乙走完全程用了48分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有1200米.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个12. 如图,直线y=x+8分别与x轴、y轴交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,当PC+PD值最小时,点P的坐标为( )
A、1个 B、2个 C、3个 D、4个12. 如图,直线y=x+8分别与x轴、y轴交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,当PC+PD值最小时,点P的坐标为( ) A、(-4,0) B、(-3,0) C、(-2,0) D、(-1,0)
A、(-4,0) B、(-3,0) C、(-2,0) D、(-1,0)二、填空题
-
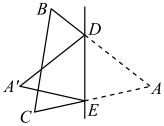
13. 25的平方根是 .14. 如图,将ABC沿着DE对折,点A落到处,若 , 则∠A=度.
 15. 汽车开始行驶时,油箱中有油30升,如果每小时耗油4升,那么油箱中的剩余油量y(升)和工作时间x(时)之间的函数关系式是;16. 如图,ABC中,直线DE是AB边的对称轴,交AC于D,交AB于E,如果BC=5,BCD的周长为15,那么AC边的长是 .
15. 汽车开始行驶时,油箱中有油30升,如果每小时耗油4升,那么油箱中的剩余油量y(升)和工作时间x(时)之间的函数关系式是;16. 如图,ABC中,直线DE是AB边的对称轴,交AC于D,交AB于E,如果BC=5,BCD的周长为15,那么AC边的长是 .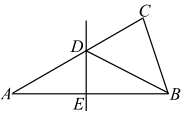 17. 有一个三角形的两边长是1和 , 要使这个三角形成为直角三角形,则第三边边长的平方是 .18. 漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,且当时间t=0min时,水位h=2cm.如表是小明记录的部分数据,其中有一个h的值记录不符合题意,请排除后利用正确的数据确定当h为8cm时,对应的时间t为min.
17. 有一个三角形的两边长是1和 , 要使这个三角形成为直角三角形,则第三边边长的平方是 .18. 漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,且当时间t=0min时,水位h=2cm.如表是小明记录的部分数据,其中有一个h的值记录不符合题意,请排除后利用正确的数据确定当h为8cm时,对应的时间t为min.
t(min)
……
1
2
3
5
……
h(cm)
……
2.4
2.8
3.4
4
……
三、解答题
-
19. 计算: .20. 已知一个数m的两个不相等的平方根分别为a+2和3a-6.(1)、求a的值;(2)、求这个数m.21. 如图,已知点A、E、B、D在同一直线上,且AE=DB,EF=BC,EFBC,∠A与∠D相等吗?请说明理由.
 22. 如图,ABC的三个顶点的坐标分别为A(1,1),B(3,2),C(2,3).
22. 如图,ABC的三个顶点的坐标分别为A(1,1),B(3,2),C(2,3). (1)、画出ABC的关于y轴对称的 .(2)、写出各顶点的坐标.(3)、求ABC的面积.23. 如图,有一个水池,水面是一个边长为16尺的正方形,在水池正中央有一根芦苇,它高出水面2尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,则水池里水的深度是多少尺?请你用所学知识解答这个问题.
(1)、画出ABC的关于y轴对称的 .(2)、写出各顶点的坐标.(3)、求ABC的面积.23. 如图,有一个水池,水面是一个边长为16尺的正方形,在水池正中央有一根芦苇,它高出水面2尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,则水池里水的深度是多少尺?请你用所学知识解答这个问题. 24. 阅读下面的材料,然后解答问题:我们新定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做可爱三角形.(1)、根据可爱三角形的定义,等边三角形是可爱三角形吗?请说明理由;(2)、若某三角形的三边长分别为2、、3,试判断该三角形是否为可爱三角形,请说明理由.25. 某市为了节约用水,采用分段收费标准、设居民每月应交水费y(元),用水量x(立方米).
24. 阅读下面的材料,然后解答问题:我们新定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做可爱三角形.(1)、根据可爱三角形的定义,等边三角形是可爱三角形吗?请说明理由;(2)、若某三角形的三边长分别为2、、3,试判断该三角形是否为可爱三角形,请说明理由.25. 某市为了节约用水,采用分段收费标准、设居民每月应交水费y(元),用水量x(立方米).用水量x(立方米)
应交水费y(元)
不超过10立方米
每立方米4元
超过10立方米
超过的部分每立方米5元
(1)、若某户居民某月用水8立方米,应交水费元;若用水15立方米,应交水费 元.(2)、求每月应交水费y(元)与用水量x(立方米)(x>10)之间的函数关系式;(3)、若某户居民某月交水费80元,则该户居民用水多少立方米?26. 如图,直线AB与x轴相交于点A,与y轴相交于点B(0,4),点C(-2,6)在直线AB上,连结OC. (1)、求直线AB对应的函数表达式和OBC的面积;(2)、点P为直线AB上一动点,AOP的面积与OBC的面积相等,求点P的坐标.27. 如图1,将两个完全相同的直角三角形纸片ACB和DEF重合放置,其中∠C=∠E=90,∠B=∠F=30°,量得它们的斜边长为8cm.
(1)、求直线AB对应的函数表达式和OBC的面积;(2)、点P为直线AB上一动点,AOP的面积与OBC的面积相等,求点P的坐标.27. 如图1,将两个完全相同的直角三角形纸片ACB和DEF重合放置,其中∠C=∠E=90,∠B=∠F=30°,量得它们的斜边长为8cm.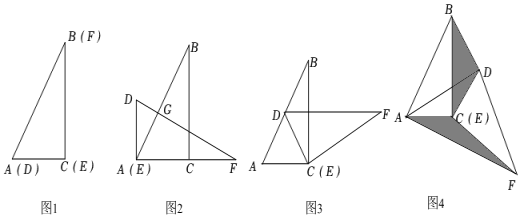 (1)、固定ACB,将DEF按如图2放置,使点A、点E重合,点C恰好在EF边上,DF与AB交于点G,求出DG的长度;(2)、固定ACB,将DEF按如图3放置,使点C、点E重合,点D恰好在AB边上,试说明线段DF与AC的位置关系;(3)、固定ACB,将DEF按如图4放置,仍然使点C、点E重合,设BDC的面积为 , AFC的面积为 , 猜想与的数量关系,并说明理由.
(1)、固定ACB,将DEF按如图2放置,使点A、点E重合,点C恰好在EF边上,DF与AB交于点G,求出DG的长度;(2)、固定ACB,将DEF按如图3放置,使点C、点E重合,点D恰好在AB边上,试说明线段DF与AC的位置关系;(3)、固定ACB,将DEF按如图4放置,仍然使点C、点E重合,设BDC的面积为 , AFC的面积为 , 猜想与的数量关系,并说明理由.