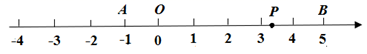山东省济南市槐荫区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-25 类型:期末考试
一、单选题
-
1. 下列各组量中,不是互为相反意义的量的是 ( )A、收入80元与支出30元 B、上升20米与下降15米 C、超过5厘米与不足3厘米 D、增大2岁与减少2升2. 为全面掌握小区居民新冠疫苗接种情况,社区工作人员设计了以下几种调查方案:
方案一:调查该小区每栋居民楼的10户家庭成员的疫苗接种情况;
方案二:随机调查该小区100位居民的疫苗接种情况;
方案三:对本小区所有居民的疫苗接种情况逐一调查统计.
在上述方案中,能较好且准确地得到该小区居民疫苗接种情况的是( )
A、方案一 B、方案二 C、方案三 D、以上都不行3. 下列各组数中,与数值-1相等的是( )A、-(-1) B、(-1)2020 C、|-1| D、-120204. 下列各图中表示线段 ,射线 的是( )A、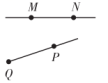
B、
B、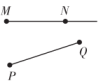
C、
C、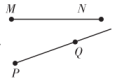
D、
D、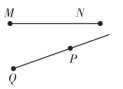
5. 下列运算正确的是( )A、 B、 C、 D、6. “绿水青山就是金山银山”.某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资元资金.数据可表示为( )A、10.12亿 B、1.012亿 C、101.2亿 D、1012亿7. 一个不透明的布袋中装有1个白球和2个红球,它们除颜色不同以外其他都相同,从布袋中任意摸出一个球是白球的概率为( )A、 B、 C、 D、18. 下列方程中, 解为的是 ( )A、 B、 C、 D、9. 下面的几何体中,哪一个不能由平面图形绕某直线旋转一周得到( )A、
5. 下列运算正确的是( )A、 B、 C、 D、6. “绿水青山就是金山银山”.某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资元资金.数据可表示为( )A、10.12亿 B、1.012亿 C、101.2亿 D、1012亿7. 一个不透明的布袋中装有1个白球和2个红球,它们除颜色不同以外其他都相同,从布袋中任意摸出一个球是白球的概率为( )A、 B、 C、 D、18. 下列方程中, 解为的是 ( )A、 B、 C、 D、9. 下面的几何体中,哪一个不能由平面图形绕某直线旋转一周得到( )A、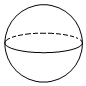 B、
B、 C、
C、 D、
D、 10. 如图,点C在线段AB上,AB=10,AC=4,点D是BC的中点,则BD的长为( )
10. 如图,点C在线段AB上,AB=10,AC=4,点D是BC的中点,则BD的长为( )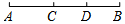 A、2 B、3 C、5 D、611.
A、2 B、3 C、5 D、611.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )
 A、35° B、70° C、110° D、145°12. 将一列有理数-1,2,-3,4,-5,6……按如图所示进行排列,则2022应排在( )
A、35° B、70° C、110° D、145°12. 将一列有理数-1,2,-3,4,-5,6……按如图所示进行排列,则2022应排在( ) A、位置 B、位置 C、位置 D、位置
A、位置 B、位置 C、位置 D、位置二、填空题
-
13. 比-4小3的数是 .14. 下列几何体:①圆柱;②正方体;③棱柱;④球;在这些几何体中截面可能是圆的有 . (只填写序号即可)15. 某校为了举办“迎国庆”的活动,调查了本校所有学生,调查的结果被整理成如图所示的扇形统计图.如果全校学生人数是1200人,根据图中给出的信息,这所学校赞成举办演讲比赛的学生有人.
 16. 如图,把一副三角板相等的两边重合摆放在一起, , , 则度.
16. 如图,把一副三角板相等的两边重合摆放在一起, , , 则度.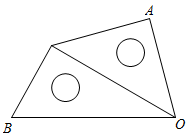 17. 五边形从某一个顶点出发可以引条对角线.18. 若 , 则的值为 .
17. 五边形从某一个顶点出发可以引条对角线.18. 若 , 则的值为 .三、解答题
-
19. 计算:(1)、(-17)+7(2)、(-14)-(-39)20. 计算:2×(-5)+23-3÷ .21. 如图,C是线段AB外一点,按要求画图:
 (1)、画射线CB;(2)、反向延长线段AB;(3)、连接AC,并延长AC至点D,使CD=AC.22. 先化简,再求值: ,其中 .23. 解方程:24. 小彬和小强每天早晨坚持跑步,小彬每秒跑4m,小强每秒跑6m.(1)、如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?(2)、如果小强站在百米跑道的起点处,小彬站在他前面10m处,两人同时同向起跑,几秒后小强能追上小彬?25. 为了加强语文课外阅读,某年级积极组织学生参加课外阅读读书分享会活动.从年级推荐的四种读物A:《水浒传》、B:《骆驼祥子》、C:《昆虫记》、D:《朝花夕拾》中选择一本读物每周一与班级同学分享读书体会。读书分享会活动组随机抽取本年级的部分学生,调查他们这四本读物中最喜爱一本读物,并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)、画射线CB;(2)、反向延长线段AB;(3)、连接AC,并延长AC至点D,使CD=AC.22. 先化简,再求值: ,其中 .23. 解方程:24. 小彬和小强每天早晨坚持跑步,小彬每秒跑4m,小强每秒跑6m.(1)、如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?(2)、如果小强站在百米跑道的起点处,小彬站在他前面10m处,两人同时同向起跑,几秒后小强能追上小彬?25. 为了加强语文课外阅读,某年级积极组织学生参加课外阅读读书分享会活动.从年级推荐的四种读物A:《水浒传》、B:《骆驼祥子》、C:《昆虫记》、D:《朝花夕拾》中选择一本读物每周一与班级同学分享读书体会。读书分享会活动组随机抽取本年级的部分学生,调查他们这四本读物中最喜爱一本读物,并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题: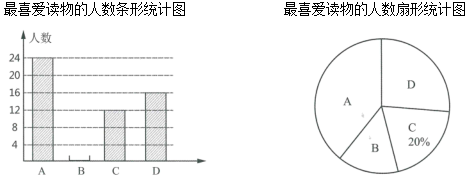 (1)、求被调查的学生人数;(2)、补全条形统计图;(3)、已知该年级有名学生,估计全年级最喜爱《水浒传》的学生有多少人?26. 某工人计划加工一批产品,如果每小时加工产品10个,就可以在预定时间完成任务,如果每小时多加工2个,就可以提前1小时完成任务.(1)、该产品的预定加工时间为几小时?(2)、若该产品销售时的标价为100元/个,按标价的八折销售时,每个仍可以盈利25元,该批产品总成本为多少元?27. 已知数轴上两点A、B对应的数分别为一1、5,点P为数轴上一动点,其对应的数为x.(1)、若点P到点A点B的距离相等,求点P对应的数是;(2)、数轴上是否存在点P,使点P到点A点B的距离之和为8?若存在,请求出x的值;若不存在,说明理由;(3)、现在点A点B分别以2个单位长度每分和1个单位长度每分的速度同时向右运动,点P以6个单位长度每分的速度向O点向左运动,当遇到A时,点P以原来的速度向右运动,并不停得往返于A与B之间,求当A遇到B重合时,P所经过的总路程.
(1)、求被调查的学生人数;(2)、补全条形统计图;(3)、已知该年级有名学生,估计全年级最喜爱《水浒传》的学生有多少人?26. 某工人计划加工一批产品,如果每小时加工产品10个,就可以在预定时间完成任务,如果每小时多加工2个,就可以提前1小时完成任务.(1)、该产品的预定加工时间为几小时?(2)、若该产品销售时的标价为100元/个,按标价的八折销售时,每个仍可以盈利25元,该批产品总成本为多少元?27. 已知数轴上两点A、B对应的数分别为一1、5,点P为数轴上一动点,其对应的数为x.(1)、若点P到点A点B的距离相等,求点P对应的数是;(2)、数轴上是否存在点P,使点P到点A点B的距离之和为8?若存在,请求出x的值;若不存在,说明理由;(3)、现在点A点B分别以2个单位长度每分和1个单位长度每分的速度同时向右运动,点P以6个单位长度每分的速度向O点向左运动,当遇到A时,点P以原来的速度向右运动,并不停得往返于A与B之间,求当A遇到B重合时,P所经过的总路程.