江西省赣州市章贡区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-25 类型：期末考试

进入出卷网下载

一、单选题

1. 若零上 $5 ° C$ 记作 $+ 5 ° C$ ，则零下 $4 ° C$ 应记作（）

A、 $- 5 ° C$ B、 $+ 5 ° C$ C、 $- 4 ° C$ D、 $+ 4 ° C$

查看试题解析
2. 这些年“舌尖上的浪费”仍有发生．疫情之下，全球近690000000人处于饥饿状态．习总书记居安思危，以身作则，亲自践行光盘行动．将数据690000000用科学记数法表示为（）

A、6.9×10⁸ B、0.69×10¹⁰ C、6.9×10⁹ D、69×10⁸

查看试题解析
3. 拿一个4倍的放大镜看一个1°的角，则这个角为（）

A、4 B、1 C、5 D、不能确定，视放大镜的距离而定

查看试题解析
4. 下列计算正确的是（）

A、2a+3a＝5a² B、5a²﹣3b²＝2a²b² C、3﹣2（a﹣2b）＝3﹣2a+4b D、2m²n﹣2n²m＝0

查看试题解析
5. 一个密封的瓶子里装着一些水（如图所示），已知瓶子的底面积为 $10 {cm}^{2}$ ，请你根据图中标明的数据，计算瓶子的容积是（） ${cm}^{3}$ ．

A、80 B、70 C、60 D、50

查看试题解析
6. 根据下表中提供的四个数的变化规律，则 $x$ 的值为（）
1
4
2
6
3
8
4
10
$n$
20
2
9
3
20
4
35
5
54
…
m
x
第1个
第2个
第3个
第4个
第 $n$ 个

A、252 B、209 C、170 D、135

查看试题解析

二、填空题

7. ﹣1的相反数是．

查看试题解析
8. 若单项式x²y³与-3x²ⁿy³是同类项，则n=.

查看试题解析
9. 已知|x+2020|+|y﹣2021|＝0，则x﹣y＝．

查看试题解析
10. 中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初日健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是：有人要去某关口，路程378里，第一天健步行走，从第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地．设此人第三天走的路程为x里，则列方程为．

查看试题解析
11. 如图，点C为线段AB上一点，AC：CB＝3：2，D、E两点分别AC、AB的中点，若线段DE＝2cm，则AB＝cm．

查看试题解析
12. 如图，点O在直线AB上，过O作射线OC，∠BOC=100°，一直角三角板的直角顶点与点O重合，边OM与OB重合，边ON在直线AB的下方．若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为．

查看试题解析

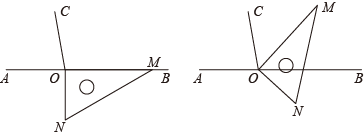
三、解答题

13.

(1)、计算：-12+（-3）²

(2)、一个角是它的余角的两倍，求这个角

查看试题解析
14. 先化简，再求值： $2 (x^{2} - x y) - 3 (x^{2} - 2 x y)$ ，其中 $x = 2$ ， $y = - 1$ ．

查看试题解析
15. 解方程： $\frac{1 - x}{2} - 2 = \frac{x}{4}$

查看试题解析
16. 如图，∠AOB＝∠COD＝90°．

(1)、∠AOC与∠BOD相等吗？请说明理由；

(2)、若∠BOD＝150°，射线OE平分∠AOC，则∠DOE等于多少度？

查看试题解析
17. 如图，由六个棱长为1cm的小正方体组成一个几何体．

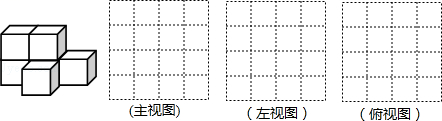(1)、分别画出这个几何体的主视图、左视图、俯视图．

(2)、该几何体的表面积是cm² ．

查看试题解析
18. 已知方程 $3 (x - \frac{1}{3}) = 2 x + 7$ 与关于 x 的方程3a-8=2（x+a）-a的解相同．

(1)、求 a 的值；

(2)、若 a、b在数轴上对应的点在原点的两侧，且到原点的距离相等，c 是倒数等于本身的数，求（a + b - c）²⁰²²的值．

查看试题解析
19. 情景：试根据图中信息，解答下列问题：

(1)、购买8根跳绳需元，购买14根跳绳需元．

(2)、小红比小明多买2根，付款时小红反而比小明少5元，你认为有这种可能吗？若有，请求出小红购买跳绳的根数；若没有，请说明理由．

查看试题解析
20. 若关于x，y的多项式 $(40 - \frac{1}{3} m) x^{2} + (- n + 2) x - 5 y + 1$ 的值与字母x取值无关．

(1)、求 $m - n^{2}$ 的值；

(2)、已知∠AOB=m°，在∠AOB内有一条射线OP，恰好把∠AOB分成1：n的两部分，求∠AOP的度数．

查看试题解析
21.

(1)、如图所示的长方体，长、宽、高分别为4，3，6．若将它的表面沿某些棱剪开，展成一个平面图形，则下列图形中，可能是该长方体表面展开图的有（填序号）．

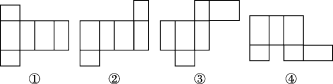(2)、图A，B分别是题（1）中长方体的两种表面展开图，求得图A的外围周长为52，请你求出图B的外围周长．

(3)、第（1）题中长方体的表面展开图还有不少，聪明的你能画出一个使外围周长最大的表面展开图吗？请画出这个表面展开图，并求出它的外围周长．

查看试题解析
22. 新定义：一个四位数，记千位上和百位上的数字之和为x，十位上和个位上的数字之和为y，如果x=y，那么称这个四位数为“幸运数”，例如：1423，x=1+4，y=2+3，因为x=y，所以1423是“幸运数”．

(1)、直接运用：最大的“幸运数”是；

(2)、提升运用：将一个“幸运数”的个位上与十位上的数字交换位置，同时将百位上与千位上的数字交换位置，称交换前后这两个“幸运数”为“相伴幸运数”．例如：1423与4132为“相伴幸运数”；设任意一个“幸运数”的千位上数字为a，百位上数字为b，十位上数字为c，个位上数字为d，请你说明“幸运数”和它的“相伴幸运数”之和一定是11的倍数；

(3)、拓展运用：请你直接写出同时满足下列条件的所有“幸运数”．
①个位上的数字是千位上的数字的两倍；
②百位上的数字与十位上的数字之和是12．

查看试题解析
23. 如图，点O为数轴的原点，A，B在数轴上按顺序从左到右依次排列，点B表示的数为8，AB=12．

(1)、直接写出数轴上点A表示的数．

(2)、动点P、Q分别从A、B同时出发，点P以每秒3个单位长度的速度沿数轴向右匀速运动，点Q以每秒2个单位长度的速度沿数轴向右匀速运动．
①经过多少秒，点P是线段OQ的中点？
②在P、Q两点相遇之前，点M为PO的中点，点N在线段OQ上，且QN= $\frac{2}{3}$ OQ．问：经过多少秒，在P、M、N三个点中其中一个点为以另外两个点为端点的线段的三等分点（把一条线段分成1：2的两条线段的点叫做这条线段的三等分点）？

查看试题解析

1	4	2	6	3	8	4	10		$n$	20
2	9	3	20	4	35	5	54	…	m	x
第1个		第2个		第3个		第4个			第 $n$ 个