广东省珠海市斗门区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-25 类型：期末考试

进入出卷网下载

一、单选题

1. 有理数 $- \frac{2}{3}$ 的相反数是（）

A、 $\frac{3}{2}$ B、 $- \frac{3}{2}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看试题解析
2. 目前，粤港澳大湾区9个地级以上市中，城际轨道交通和城市轨道交通已开通运营总里程超过1100公里，规划总里程近6000公里，数6000用科学记数法表示为（）

A、6×10³ B、6×10⁴ C、0.6×10⁴ D、60×10²

查看试题解析
3. 下列方程是一元一次方程的是（）

A、2x＋3y＝7 B、3x²＝3 C、6＝ $\frac{2}{x}$ －1 D、2x－1＝20

查看试题解析
4. 如图，射线 $O A$ 表示的方向是（）

A、东偏南 $55 °$ B、南偏东 $35 °$ C、北偏西 $35 °$ D、南偏东 $55 °$

查看试题解析
5. 下列运算中，正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $a + 2 a = 3 a^{2}$ C、 $a^{2} + a^{3} = a^{5}$ D、 $x^{2} y - 2 x^{2} y = - x^{2} y$

查看试题解析
6. 下列四个几何体中，是四棱锥的是（）

A、 B、 C、 D、

查看试题解析
7. 已知 $x = 3$ 是关于x的方程 $ax + 2 x - 3 = 0$ 的解，则a的值为 $($ $)$

A、 $- 1$ B、 $- 2$ C、 $- 3$ D、1

查看试题解析
8. 下列说法正确的是（）

A、单项式3xy³的次数是3 B、单项式 $- \frac{x^{2} y}{2}$ 的系数是﹣2 C、多项式3x²y﹣2xy的次数是3 D、多项式4x³y+xy的系数是4

查看试题解析
9. 实数a、b在数轴上的位置如图所示，则下列说法正确的是（）

A、a+b＞0 B、a﹣b＞0 C、ab＞0 D、|a|＞|b|

查看试题解析
10. 某制药厂制造一批药品，如用旧工艺，则废水排量要比环保限制的最大量还多100t；如用新工艺，则废水排量比环保限制的最大量少50t．新、旧工艺的废水排量之比为3∶4，求两种工艺的废水排量各是多少？若设新、旧工艺的废水排量分别为 $3 x t$ 和 $4 x t$ ，则依题意列方程为（）．

A、 $3 x + 50 = 4 x - 100$ B、 $3 x - 50 = 4 x + 100$ C、 $3 x + 50 = 4 x + 100$ D、 $3 x - 50 = 4 x - 100$

查看试题解析

二、填空题

11. 若盈利8万元记作+8万元，则亏损7万元记作万元．

查看试题解析
12. 若﹣2x²yb与 $\frac{1}{2}$ xay³是同类项，则a﹣b＝．

查看试题解析
13. 如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“国”字一面的相对面上的字是．

查看试题解析
14. 一个角为 $24 ° 40^{'}$ ，则它的余角度数为．

查看试题解析
15. 若x﹣2y＝﹣6，则代数式3+2x﹣4y＝．

查看试题解析
16. 如图，用围棋子按某种规律摆成的一行“七”字，按照这种规律，第n个“七”字中的围棋子有个 $.$

查看试题解析
17. 如图是由六个不同颜色的正方形组成的长方形，已知中间最小的一个正方形A的边长为2，那么正方形B的面积是．

查看试题解析

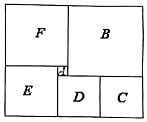
三、解答题

18. 计算：（﹣2）³÷4﹣（﹣1）²⁰²¹+|﹣6|．

查看试题解析
19. 解方程： $\frac{x - 1}{2} - \frac{2 x - 1}{3} =$ 1．

查看试题解析
20. 如图，已知DB＝2，AC＝10，点D为线段AC的中点，求线段BC的长度．

查看试题解析
21. 设 $a ， b ， c ， d$ 为实数，则我们把形如 $| \begin{array}{l} a & b \\ c & d \end{array} |$ 的式子叫做二阶行列式，它的运算法则用公式表示为 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，请利用此法则解决以下问题：

(1)、求 $| \begin{array}{l} 1 & 2 \\ - 1 & 2 \end{array} |$ 的值；

(2)、若 $| \begin{array}{l} 2 & 3 \\ 1 - x & 5 \end{array} | = 22$ ，求 $x$ 的值.

查看试题解析
22. 小刚同学由于粗心，把“2A﹣B”看成了“A﹣B”，算出A﹣B的结果为x²+x﹣4，其中B＝3x²﹣2x+1．

(1)、求A所表示的代数式；

(2)、若x＝﹣1，求代数式2A﹣B的值．

查看试题解析
23. 某校七年级准备组织观看电影《长津湖》，由各班班长负责买票，票价每张为20元，售票员说：30人以上的团体票有两个优惠方案可选择：
方案一：全体人员可打8折；
方案二：若打9折，有5人可以免票．

(1)、若1班有40名学生，则选择方案一需付元，选择方案二需付元；

(2)、若2班选择方案二需付810元，则2班有名学生；

(3)、3班班长思考了一会儿，说我们班无论选择哪种方案要付的钱是一样的，请问3班有多少人？

查看试题解析
24. 如图1，将长方形ABEF的一角向长方形内部折叠，使角的顶点A落在点 $A ′$ 处，OC为折痕，则OC平分 $∠ A O A^{'}$ ．

(1)、若∠AOC＝25°，求 $∠ A O B$ 的度数；

(2)、若点D在线段BE上，角OBD沿着折痕OD折叠落在点 $B ′$ 处，且点 $B ′$ 在长方形内．
①如果点 $B ′$ 刚好在线段 $A^{'} O$ 上，如图2所示，求∠COD的度数；
②如果点 $B ′$ 不在线段 $A^{'} O$ 上，且 $∠ A O B$ ＝40°，求∠AOC+∠BOD的度数．

查看试题解析
25. 如图1，在数轴上，点O为原点，点A表示的数为a，点B表示的数为b，且a、b满足（a+2）²+|b﹣3|＝0．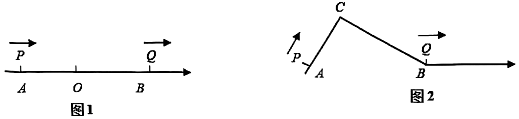

(1)、A、B两点对应的数分别为a= ， b=

(2)、动点P、Q分别从A、B两点同时出发向数轴正方向运动，点P的速度为每秒3个单位长度，点Q的速度为每秒2个单位长度，如图1所示．
①求点P追上点Q所用的时间，并求出此时点P所对应的数为多少；

②若在运动开始时，在线段AB之间找一点C，把线段AB折起，如图2所示，点P在线段AC的速度为每秒2个单位长度，在线段BC的速度为每秒4个单位长度，P、Q两点在其他位置的速度与原来相同．此时点P追上点Q所用的时间与①中所用的时间相同，求出折起前点C所对应的数为多少．

查看试题解析