广东省肇庆市封开县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-25 类型：期末考试

进入出卷网下载

一、单选题

1. 在﹣3，﹣2，1，4中，绝对值最小的数是（）

A、4 B、﹣3 C、﹣2 D、1

查看试题解析
2. 袁隆平院士被誉为“杂交水稻之父”，经过他带领的团队多年艰苦努力，目前我国杂交水稻种植面积达2.4亿亩，每年增产的粮食可以养活80000000人.将80000000这个数用科学记数法可表示为 $8 \times 10^{n}$ ，则 $n$ 的值是（）

A、6 B、7 C、8 D、9

查看试题解析
3. 下列各式中，不是整式的是（）

A、 $\frac{1}{x}$ B、 $x - y$ C、 $- \frac{x y}{6}$ D、 $4 x$

查看试题解析
4. 方程 $2 x = - 4$ 的解是（）

A、 $x = - 2$ B、 $x = 2$ C、 $x = \frac{1}{2}$ D、 $x = - 6$

查看试题解析
5. 一个角的度数等于60°20′，那么它的余角等于（）

A、40°80′ B、39°80′ C、30°40′ D、29°40′

查看试题解析
6. 下列叙述正确的是（）

A、延长直线 $A B$ 到点C B、 $30 °$ 和 $60 °$ 互为余角 C、5.1625精确到百分位是5.163 D、两点之间，直线最短

查看试题解析
7. 如果A，B，C三点同在一直线上，且线段AB＝6cm，BC＝3cm，A，C两点的距离为d，那么d＝（）

A、9cm B、3cm C、9cm或3cm D、大小不定

查看试题解析
8. 若 $20 + x + y = - 2$ ，则 $20 - x - y$ 的值为（）

A、－42 B、42 C、－2 D、22

查看试题解析
9. 下面说法中 ① $- a$ 一定是负数；② $0.3 x y$ 是二次单项式；③倒数等于它本身的数是±1；④若 $| a | = - a$ ，则 $a \leq 0$ ；⑤由 $- (x - 3) = 2$ 可变形为 $x - 3 = - 2$ ，其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 已知整数 $a_{1}$ 、 $a_{2}$ 、 $a_{3}$ 、 $a_{4}$ 、……满足下列条件： $a_{1} = - 1$ ， $a_{2} = - | a_{1} + 2 |$ ， $a_{3} = - | a_{2} + 3 |$ ， $a_{4} = - | a_{3} + 4 |$ ， …， ${a_{n}}_{+ 1} = - | a_{n} + n + 1 |$ （n为正整数）依此类推，则 $a_{2022}$ 的值为（）

A、-1010 B、-2020 C、-1011 D、-2022

查看试题解析

二、填空题

11. $\sqrt{{(- 7)}^{2}}$ 的相反数是.

查看试题解析
12. 计算： $x^{5} y^{3} - \frac{1}{3} x^{5} y^{3} =$ ．

查看试题解析
13. 如图，∠AOB=60°，∠AOC=40°，OD、OE分别平分 $∠ A O B$ 和 $∠ A O C$ ，则 $∠ D O E =$ °．

查看试题解析
14. 已知一个角的补角是它余角的3倍，那么这个角等于°．

查看试题解析
15. 已知|x﹣4|+（y+2）²＝0，则x+y的值是．

查看试题解析
16. 若方程 $3 x + 6 = 12$ 的解也是 $6 x + 3 a = 24$ 的解，则 $a$ 的值为．

查看试题解析
17. 如如图，长方形ABCD中，AB=4cm，BC=3cm，点E是CD的中点，动点P从A点出发，以每秒1cm的速度沿A→B→C运动，最终到达点C，点P运动的时间为x秒．若x＞4，那么x=秒时，△APE的面积等于5cm² ．

查看试题解析

三、解答题

18. 计算： ${(- 1)}^{10} \times 2 + {(- 2)}^{3} \div 4$ ．

查看试题解析
19. 在数轴上表示数：−2，− $\frac{1}{2}$ ， 0，1 $\frac{1}{2}$ ， −1.5，按从小到大的顺序用＜连接起来．

查看试题解析
20. 解方程： $\frac{3 x - 1}{4} - 1 = \frac{5 x - 7}{6}$

查看试题解析
21. 已知a，b互为倒数，c，d互为相反数， $| n | = 3$ ，求代数式 $\frac{2 c + 2 d - n}{a b}$ 的值．

查看试题解析
22. 某某种圆珠笔的售价是每支2元，甲、乙两家文具店均有促销活动：甲文具店全部九折；乙文具店20支及以内不打折，比20支多的部分打八折．设小明需要购买的圆珠笔的数量为x，根据题意回答下列问题：

(1)、若购买多于20支的圆珠笔，则在甲文具店需要花费元，在乙文具店需要花费元；（用含x的式子表示）

(2)、当x=25时，选择哪家文具店更优惠？

查看试题解析
23. 如图，半径为1个单位长度的圆形纸片上有一点 $Q$ 与数轴上的原点重合.（提示：圆的周长 $C = 2 π r ， π$ 取值为3.14）

(1)、把圆形纸片沿数轴向左滚动1周，点 $Q$ 到达数轴上点 $A$ 的位置，则点 $A$ 表示的数是；

(2)、圆形纸片在数轴上向右滚动的周数记为正数，圆形纸片在数轴上向左滚动的周数记为负数，依次运动情况记录如下： $+ 2 ， - 1 ， - 5 ， + 4 ， + 3 ， - 2$ .当圆形纸片结束运动时， $Q$ 点运动的路程共是多少？此时点 $Q$ 所表示的数是多少？

查看试题解析
24. 已知，O是直线AB上的一点，OC⊥OE．

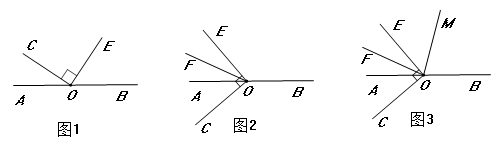(1)、如图①，若∠COA＝34°，求∠BOE的度数．

(2)、如图②，当射线OC在直线AB下方时，OF平分∠AOE，∠BOE＝130°，求∠COF的度数．

(3)、在（2）的条件下，如图③，在∠BOE内部作射线OM，使∠COM+ $\frac{17}{10}$ ∠AOE＝2∠BOM+∠FOM，求∠BOM的度数．

查看试题解析
25. 如图，在数轴上有两个长方形ABCD和EFGH，这两个长方形的宽都是3个单位长度，长方形ABCD的长AD是6个单位长度，长方形EFGH的长EH是10个单位长度，点E在数轴上表示的数是5.且E、D两点之的距离为14.

(1)、填空：点H在数轴上表示的数是.点A在数轴上表示的数是.

(2)、若线段AD的中点为M，线段EH上一点N，EN= $\frac{1}{5}$ EH，M以每秒4个单位的速度向右匀速运动，N以每秒3个单位的度向左运动，设运动时间为x秒，原点为O，当OM=ON时，求x的值.

(3)、若长方形ADCD以每秒4个单位的速度向右运动.长方形FGH固定不动.设长方形ABCD运动的时t（t＞0）秒，两个长方形重叠部分的面积为S，当S=12时，求此时t的值.

查看试题解析