广东省深圳市南山区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-25 类型：期末考试

进入出卷网下载

一、单选题

1. $- \frac{1}{5}$ 的相反数是（）

A、 $\frac{1}{5}$ B、﹣5 C、5 D、 $\frac{1}{25}$

查看试题解析
2. 2021年上半年广东各市GDP已经出炉，深圳以14324.47亿的总量继续保持榜首位置.14324.47亿可以用科学记数法表示为（）

A、14.32447×10¹¹ B、1.4×10¹² C、1.432447×10¹² D、0.1432447×10¹³

查看试题解析
3. 下列式子中正确的是（）

A、﹣|﹣31|＝31 B、（﹣5）＋（﹣5）＋（﹣5）＋（﹣5）＋（﹣5）＝（﹣5）⁵ C、﹣8÷（2﹣4）＝﹣4＋2＝﹣2 D、|﹣3﹣1|＝|﹣3|＋|﹣1|

查看试题解析
4. 下列调査最适合普查的是（）

A、调查某中学适宜接种新冠疫苗人员的实际接种情况 B、调查国庆期间全国观众最喜爱的电影 C、调查“深圳读书月”活动中市民的读书情况 D、了解一批哈密瓜是否甜

查看试题解析
5. 下列说法不正确的是（）

A、 $- \frac{3 π a^{3}}{10}$ 的系数是 $- \frac{3}{10} π$ B、x²﹣2xy＋y²是二次三项式 C、a可以表示负数，a的系数为0 D、﹣1是单项式

查看试题解析
6. 如图，下列说法不正确的是（）

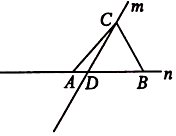A、直线m与直线n相交于点D B、点A在直线n上 C、DA＋DB＜CA＋CB D、直线m上共有两点

查看试题解析
7. 一个正方体的表面分别标有百、年、峥、嵘、岁、月，下面是该正方体的一个展开图，已知“嵘”的对面为“岁”，则（）

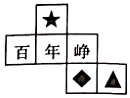A、▲代表“岁” B、▲代表“月” C、★代表“月” D、◆代表“月”

查看试题解析
8. 在光明区举办的“周年艺术季”期间，小颖一家去欣赏了一台音乐剧，路上预计用时25分钟，但由于堵车，所以实际车速比预计的每小时慢了10千米，且路上多用了5分钟．设预计车速为x千米/时，根据题意可列方程为（）

A、 $\frac{25}{60} x = \frac{30}{60} (x + 10)$ B、 $\frac{25}{60} (x + 10) = \frac{30}{60} x$ C、25x＝30x﹣10 D、 $\frac{25}{60} x = \frac{30}{60} (x - 10)$

查看试题解析
9. 数轴上点A，B表示的数分别为a，b，位置如图所示，下列式子中计算结果为负数的是（）

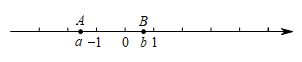A、b²﹣b B、﹣a＋b C、|ab|＋0.3 D、﹣1﹣a

查看试题解析
10. 对于代数式 $\frac{y^{2} - 1}{2}$ ，第三学习小组讨论后得出如下结论：①代数式还可以写成 $\frac{y^{2}}{2} - \frac{1}{2}$ ；②如图，较大正方形的边长为y，较小正方形的边长为1，则代数式表示阴影部分的面积；③其可以叙述为：y与1的平方差的一半；④代数式的值可能是﹣1，其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

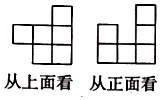
11. 若单项式3a^mb⁶与﹣8a³b^n＋²是同类项，则m﹣n＝．

查看试题解析
12. 由若干大小相同的小立方块搭成的几何体从上面和正面看到的形状如图所示，则这个几何体的小立方块最少是个．

查看试题解析
13. 若x＝﹣3是关于x的方程ax＋1＝x的解，则a＝．

查看试题解析
14. 如图，点C是线段AB的中点，CD $= \frac{1}{3}$ AC，若CB﹣CD＝8cm，则AB＝cm．

查看试题解析
15. 如图是2021年7月份的日历表，用形如的框架框住日历表中的五个数，对于框架框住的五个数字之和，小明的计算结果有45，55，60，75，小华说有结果是不正确的．通过计算，可知小明的计算结果中不正确的是．

查看试题解析

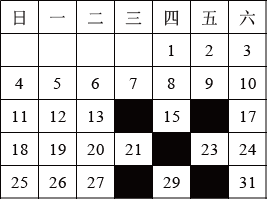
三、解答题

16. 计算：

(1)、 $1 + \frac{2}{3} - \frac{9}{4}$

(2)、 $- 32 \times \frac{1}{3} - 12 \times (\frac{5}{4} - \frac{1}{6})$

查看试题解析
17. 先化简，再求值： $\frac{1}{7} (3 a^{2} - 21 a b) - (- \frac{4}{7} a^{2} + \frac{1}{2} a b)$ ，其中a＝﹣2，b＝1

查看试题解析
18. 解下列方程：

(1)、5x﹣3（x﹣1）＝9﹣2（x＋1）

(2)、 $\frac{x + 14}{5} = \frac{2 x + 2}{3} - x$

查看试题解析
19. 如图，已知∠AOB＝120°，OE平分∠AOB，反向延长边OB至点D，再画∠COE＝70°．

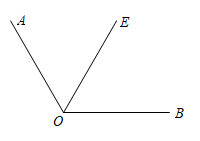(1)、请在图中补画出完整图形；

(2)、结合图形，求出∠DOC的度数．

查看试题解析
20. 下面是某公司2019年和2020年的总支出情况：
年份
2019
2020
总支出/万元
20
28
为了解2020年公司的各项开支，财务部的小张和小李又分别作出了总支出的分配情况的条形图和扇形图（均未画全）：

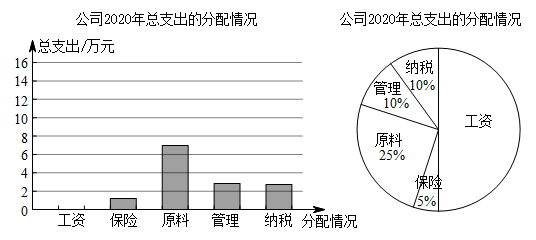(1)、请你补全条形统计图；

(2)、计算扇形统计图中原料所在扇形的圆心角度数；

(3)、2019年公司的工资支出占总支出的65%，2020年相比2019年，该公司在工资方面的金额支出是增加了还是减少了？请计算说明．

查看试题解析
21. 寒假前，七（1）班准备印制一些宪法宣传小册子，利用假期到公园里开展法制宣传活动，有甲、乙两家印刷店可供选择，两家收费情况如下：
印刷店
设计费/元
印刷单价/（元/册）
甲
8
3.55
乙
10
3.5

(1)、请你替班长计算一下，印刷多少册，两家的印刷总费用是相等的？

(2)、乙店得知同学们用零花钱集资印刷宣传册后，将印刷单价给予打折优惠，这样，七（1）班花费220元即可印刷80册．请你计算一下，乙店是打几折优惠的？

(3)、精打细算的小明通过计算得出：即使甲店给出与（2）中乙店同样的优惠，也印刷80册，还是要选择乙店．你是否同意小明的说法？请说明理由．

查看试题解析
22. 如图，P是线段AB上不同于点A，B的一点，AB＝18cm，C，D两动点分别从点P，B同时出发，在线段AB上向左运动（无论谁先到达A点，均停止运动），点C的运动速度为1cm/s，点D的运动速度为2cm/s．

(1)、若AP＝PB，
①当动点C，D运动了2s时，AC＋PD＝cm；

②当C，D两点间的距离为5cm时，则运动的时间为s；

(2)、当点C，D在运动时，总有PD＝2AC，·
①求AP的长度；
②若在直线AB上存在一点Q，使AQ﹣BQ＝PQ，求PQ的长度．

查看试题解析

印刷店	设计费/元	印刷单价/（元/册）
甲	8	3.55
乙	10	3.5

年份	2019	2020
总支出/万元	20	28