广东省揭阳市普宁市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-25 类型:期末考试
一、单选题
-
1. 点A在数轴上的位置如图所示,则点A表示的数的相反数为( )
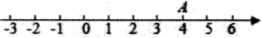 A、4 B、 C、 D、2. 如右图,是由四个大小相同的小正方体组成的几何体,从上面看这个几何体得到的平面图形是( )
A、4 B、 C、 D、2. 如右图,是由四个大小相同的小正方体组成的几何体,从上面看这个几何体得到的平面图形是( ) A、
A、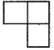 B、
B、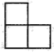 C、
C、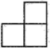 D、
D、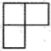 3. 数据27500亿用科学记数法表示为( )A、 B、 C、 D、4. 如图,对于直线 ,线段 ,射线 ,其中能相交的是( ).A、
3. 数据27500亿用科学记数法表示为( )A、 B、 C、 D、4. 如图,对于直线 ,线段 ,射线 ,其中能相交的是( ).A、 B、
B、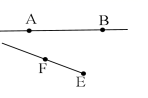 C、
C、 D、
D、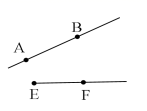 5. 调查下列问题时,适合采用普查的是( )A、了解一批圆珠笔芯的使用寿命 B、了解我市七年级学生的视力情况 C、了解一批西瓜是否甜 D、神舟十二号载人飞船发射前对重要零部件的检查6. 下列整式运算不正确的是( )A、 B、 C、 D、7. 如图,将正方体沿面AB′C剪下,则截下的几何体为( )
5. 调查下列问题时,适合采用普查的是( )A、了解一批圆珠笔芯的使用寿命 B、了解我市七年级学生的视力情况 C、了解一批西瓜是否甜 D、神舟十二号载人飞船发射前对重要零部件的检查6. 下列整式运算不正确的是( )A、 B、 C、 D、7. 如图,将正方体沿面AB′C剪下,则截下的几何体为( ) A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱8. 下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A、
A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱8. 下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A、 B、
B、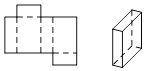 C、
C、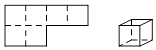 D、
D、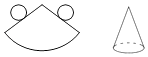 9. 如图,小明将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为( )
9. 如图,小明将一个正方形纸片剪去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为( )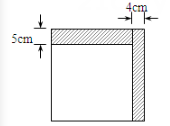 A、16 B、20 C、80 D、16010. 将一副三角板如图①的位置摆放,其中30°直角三角板的直角边与等腰直角三角板的斜边重合,30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合(为点O).现将30°的直角三角板绕点O顺时针旋转至如图②的位置,此时为25°,则( )
A、16 B、20 C、80 D、16010. 将一副三角板如图①的位置摆放,其中30°直角三角板的直角边与等腰直角三角板的斜边重合,30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合(为点O).现将30°的直角三角板绕点O顺时针旋转至如图②的位置,此时为25°,则( )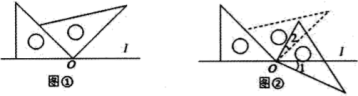 A、15° B、20° C、25° D、30°
A、15° B、20° C、25° D、30°二、填空题
-
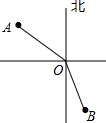
11. 的绝对值是 , 的倒数是 .12. 已知单项式2abn﹣1与是同类项,则2m+n= .13. 如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB= .
 14. 如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是度.
14. 如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是度.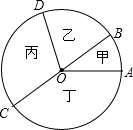 15. 已知 , , 则代数式的值为 .16. 某商品的进价是2000元,标价为2800元,该商品打多少折才能获得12%的利润率?设该商品需打x折才能使利润率为12%,根据题意列出方程: .17. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次点A向左移动3个单位长度到达点 , 第2次从点向右移动6个单位长度到达点 , 第3次从点向左移动9个单位长度到达点 , …,按照这种移动规律进行下去,第n次移动到达点 , 如果点与原点的距离不小于17,那么n的最小值是 .
15. 已知 , , 则代数式的值为 .16. 某商品的进价是2000元,标价为2800元,该商品打多少折才能获得12%的利润率?设该商品需打x折才能使利润率为12%,根据题意列出方程: .17. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次点A向左移动3个单位长度到达点 , 第2次从点向右移动6个单位长度到达点 , 第3次从点向左移动9个单位长度到达点 , …,按照这种移动规律进行下去,第n次移动到达点 , 如果点与原点的距离不小于17,那么n的最小值是 .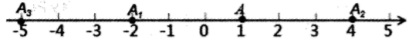
三、解答题
-
18. 计算:19. 解方程:20. 如图,已知线段AB和点P,请用尺规按照下列要求作图:(不必写作法,但需保留作图痕迹)
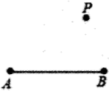 (1)、延长线段AB到C,使得;(2)、连接PC;作射线AP;(3)、如果cm,求AC的值.21. 先化简,再求值: , 其中、满足 .22. 一家公司对一种新研发的产品进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级对该产品进行评价,图1和图2是该公司采集数据后,绘制的两幅不完整的统计图,请你根据以下统计图提供的信息,回答下列问题:
(1)、延长线段AB到C,使得;(2)、连接PC;作射线AP;(3)、如果cm,求AC的值.21. 先化简,再求值: , 其中、满足 .22. 一家公司对一种新研发的产品进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级对该产品进行评价,图1和图2是该公司采集数据后,绘制的两幅不完整的统计图,请你根据以下统计图提供的信息,回答下列问题: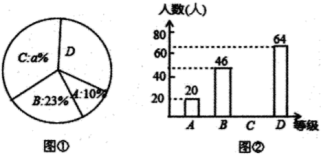 (1)、本次调查的人数为多少人?C等级的人数是多少?请在图中补全条形统计图;(2)、图①中,a等于多少?D等级所占的圆心角为多少度?23. 用“△”定义一种新运算:对于任意有理数a和b,规定 , 如:(1)、求的值;(2)、若 , 求x的值.24. 已知如图,在数轴上有A,B两点,所表示的数分别为 , , 点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,如果设运动时间为t秒,解答下列问题:
(1)、本次调查的人数为多少人?C等级的人数是多少?请在图中补全条形统计图;(2)、图①中,a等于多少?D等级所占的圆心角为多少度?23. 用“△”定义一种新运算:对于任意有理数a和b,规定 , 如:(1)、求的值;(2)、若 , 求x的值.24. 已知如图,在数轴上有A,B两点,所表示的数分别为 , , 点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,如果设运动时间为t秒,解答下列问题: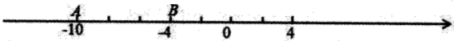 (1)、运动前线段AB的长为;运动1秒后线段AB的长为;(2)、运动t秒后,点A,点B在数轴上表示的数分别为和 ;(用含t的代数式表示)(3)、求t为何值时,点A与点B恰好重合;(4)、在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为5,若存在,求t的值;若不存在,请说明理由.25. 已知 为直线 上一点,射线 、 、 位于直线 上方, 在 的左侧, , .
(1)、运动前线段AB的长为;运动1秒后线段AB的长为;(2)、运动t秒后,点A,点B在数轴上表示的数分别为和 ;(用含t的代数式表示)(3)、求t为何值时,点A与点B恰好重合;(4)、在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为5,若存在,求t的值;若不存在,请说明理由.25. 已知 为直线 上一点,射线 、 、 位于直线 上方, 在 的左侧, , .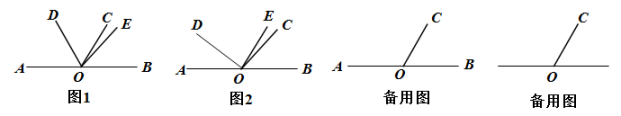 (1)、如图1, , 当 平分 时,求 的度数.(2)、如图2,若 , 且 , 求 (用 表示).(3)、若 , 点 在射线 上,若射线 绕点 顺时针旋转 ( ), , 平分 , 当 时,求 的值.
(1)、如图1, , 当 平分 时,求 的度数.(2)、如图2,若 , 且 , 求 (用 表示).(3)、若 , 点 在射线 上,若射线 绕点 顺时针旋转 ( ), , 平分 , 当 时,求 的值.