广东省揭阳市揭东区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-25 类型:期末考试
一、单选题
-
1. 单项式-3πxy2z3的系数和次数分别是 ( )
A、-π,5 B、-1,6 C、-3π,6 D、-3,72. 按照知情同意自愿的原则,我国正积极引导3岁至11岁适龄无禁忌人群“应接尽接”,截至10月29日,该人群已接种新冠疫苗超过353万剂次,则353万用科学记数法表示为( )A、 B、 C、 D、3. 下列是由4个大小相同的小立方块搭成的几何体,从正面和从左面看得到的形状图相同的是( )A、 B、
B、 C、
C、 D、
D、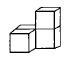 4. 以下问题,不适合全面调查的是( )A、调查和一新冠肺炎感染者密切接触人群 B、调查我市中学生心理健康现状 C、检测长征运载火箭的零部件质量情况 D、调查某中学在职教师的身体健康状况5. 嘉琪同学在计算时,运算过程正确且比较简便的是( )A、 B、 C、 D、6. 同一条直线上三点 , , 则的长度为( )A、 B、或 C、或 D、或7. 已知关于x的方程是一元一次方程,则m的值为( )A、1 B、-1 C、1或-1 D、以上结果均错误8. 如图1所示,在一个边长为a的正方形纸片上剪去两个小长方形,得到一个如图2的图案所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为( )
4. 以下问题,不适合全面调查的是( )A、调查和一新冠肺炎感染者密切接触人群 B、调查我市中学生心理健康现状 C、检测长征运载火箭的零部件质量情况 D、调查某中学在职教师的身体健康状况5. 嘉琪同学在计算时,运算过程正确且比较简便的是( )A、 B、 C、 D、6. 同一条直线上三点 , , 则的长度为( )A、 B、或 C、或 D、或7. 已知关于x的方程是一元一次方程,则m的值为( )A、1 B、-1 C、1或-1 D、以上结果均错误8. 如图1所示,在一个边长为a的正方形纸片上剪去两个小长方形,得到一个如图2的图案所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为( ) A、 B、 C、 D、9. 如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识探究,这7个数的和不可能是( )
A、 B、 C、 D、9. 如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识探究,这7个数的和不可能是( ) A、168 B、140 C、98 D、6310. 如图,将一张长方形纸片ABCD沿对角线BD折叠后,点C落在点E处,连接BE交AD于F,再将三角形DEF沿DF折叠后,点E落在点G处,若DG刚好平分∠ADB,那么∠ADB的度数是( )
A、168 B、140 C、98 D、6310. 如图,将一张长方形纸片ABCD沿对角线BD折叠后,点C落在点E处,连接BE交AD于F,再将三角形DEF沿DF折叠后,点E落在点G处,若DG刚好平分∠ADB,那么∠ADB的度数是( )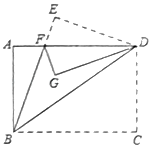 A、18° B、20° C、36° D、45°
A、18° B、20° C、36° D、45°二、填空题
-
11. 若a,b互为相反数,则(a+b﹣1)2016= .12. 计算 .13. 一个多边形从同一个顶点引出的对角线,将这个多边形分成7个三角形.则这个多边形有条边.14. 若mn=m+3,则2mn+3m-5nm+10=.15. 用一个平面去截一个正方体,得到的截面的形状可能是:①圆,②三角形,③长方形,④五边形,⑤六边形,⑥七边形其中的 .16. 如图,将一副三角板按如图所示的位置摆放,若O,C两点分别放置在直线AB上,则∠AOE=度.
 17. 一只兔子落在数轴的某点P0上,第1次从P0向左跳1个单位到P1 , 第2次从P1向右跳2个单位到P2 , 第3次从P2向左跳3个单位到P3 , 第4次从P3向右跳4个单位到P4 , …,若按以上规律跳了100次时,兔子落在数轴上的点P100所表示的数恰好是2021,则这只兔子的初始位置P0所表示的数是 .
17. 一只兔子落在数轴的某点P0上,第1次从P0向左跳1个单位到P1 , 第2次从P1向右跳2个单位到P2 , 第3次从P2向左跳3个单位到P3 , 第4次从P3向右跳4个单位到P4 , …,若按以上规律跳了100次时,兔子落在数轴上的点P100所表示的数恰好是2021,则这只兔子的初始位置P0所表示的数是 .三、解答题
-
18. 计算: .19. 解方程:.20. 先化简,再求值:已知2(a2b+ab)﹣2(a2b﹣1)﹣2ab2﹣2,其中a=﹣2,b=2.21. 如图1,已知 ,有一个三角板BDE与 共用一个顶点B,其中 .
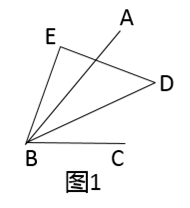 (1)、若BD平分 ,求 的度数;(2)、如图2,将三角板绕着点B顺时针旋转 度( ),当 时,求 的度数.
(1)、若BD平分 ,求 的度数;(2)、如图2,将三角板绕着点B顺时针旋转 度( ),当 时,求 的度数.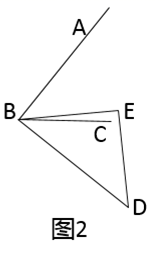 22. 定义新运算“@”与“ ”: ,(1)、计算 的值;(2)、若 ,比较A和B的大小23. 某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
22. 定义新运算“@”与“ ”: ,(1)、计算 的值;(2)、若 ,比较A和B的大小23. 某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题: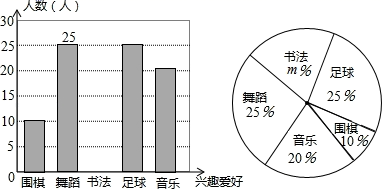 (1)、学校这次调查共抽取了名学生;(2)、求m的值并补全条形统计图;(3)、在扇形统计图中,“围棋”所在扇形的圆心角度数为;(4)、设该校共有学生 名,请你估计该校有多少名学生喜欢足球.24. 为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现,甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球,乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)、求每套队服和每个足球的价格是多少?(2)、若城区四校联合购买100套队服和 个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;(3)、在(2)的条件下,若 ,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?25. 如图,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米.P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,终点为C;点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,终点为B.如果P、Q同时出发,用t(秒)表示移动时间.
(1)、学校这次调查共抽取了名学生;(2)、求m的值并补全条形统计图;(3)、在扇形统计图中,“围棋”所在扇形的圆心角度数为;(4)、设该校共有学生 名,请你估计该校有多少名学生喜欢足球.24. 为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现,甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球,乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)、求每套队服和每个足球的价格是多少?(2)、若城区四校联合购买100套队服和 个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;(3)、在(2)的条件下,若 ,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?25. 如图,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米.P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,终点为C;点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,终点为B.如果P、Q同时出发,用t(秒)表示移动时间. (1)、分别求出P、Q到达终点时所需时间;(2)、若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP;(3)、当t为何值时,三角形QBC的面积等于三角形ABC面积的 .
(1)、分别求出P、Q到达终点时所需时间;(2)、若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP;(3)、当t为何值时,三角形QBC的面积等于三角形ABC面积的 .