广东省河源市紫金县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-25 类型:期末考试
一、单选题
-
1. 2021的相反数是( )A、 B、 C、 D、2. 庆祝新中国成立72周年,国庆假期期间,各旅游景区节庆氛围浓厚,某景区同步设置的“我为祖国点赞”装置共收集约6390000个“赞”,这个数字用科学记数法可表示为( )A、6.39×106 B、0.639×106 C、0.639×107 D、6.39×1053. 已知3是关于x的方程的解,则a的值是( )A、 B、5 C、7 D、24. 如图,是一个正方体的表面展开图,则原正方体中“爱”字所对应的面相对的面上标的字是( )
 A、我 B、的 C、祖 D、国5. 单项式 的次数是( )A、8 B、7 C、5 D、6. 如图所示,用一个平面分别去截下列水平放置的几何体,所截得的截面不可能是三角形的是( )A、
A、我 B、的 C、祖 D、国5. 单项式 的次数是( )A、8 B、7 C、5 D、6. 如图所示,用一个平面分别去截下列水平放置的几何体,所截得的截面不可能是三角形的是( )A、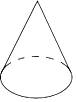 B、
B、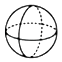 C、
C、 D、
D、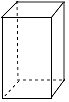 7. 下列调查中,适宜抽样调查的是( )A、了解某批次灯泡的使用寿命 B、了解长征五号运载火箭零件的质量 C、在“新冠状肺炎”疫情期间,对出入某小区的人员进行体温检测 D、了解全班同学的血型8. 把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设这个班有 名学生,则依题意所列方程正确的是( ).A、 B、 C、 D、9. 如图所示,钟表上9:30时,时针与分针之间所成的角是( )
7. 下列调查中,适宜抽样调查的是( )A、了解某批次灯泡的使用寿命 B、了解长征五号运载火箭零件的质量 C、在“新冠状肺炎”疫情期间,对出入某小区的人员进行体温检测 D、了解全班同学的血型8. 把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设这个班有 名学生,则依题意所列方程正确的是( ).A、 B、 C、 D、9. 如图所示,钟表上9:30时,时针与分针之间所成的角是( ) A、60° B、90° C、105° D、120°10. 已知a1+a2=1,a2+a3=2,a3+a4=﹣3,a4+a5=﹣4,a5+a6=5,a6+a7=6,a7+a8=﹣7,a8+a9=﹣8,……,a99+a100=﹣99,a100+a1=﹣100,那么a1+a2+a3+……+a100的值为( )A、﹣48 B、﹣50 C、﹣98 D、﹣100
A、60° B、90° C、105° D、120°10. 已知a1+a2=1,a2+a3=2,a3+a4=﹣3,a4+a5=﹣4,a5+a6=5,a6+a7=6,a7+a8=﹣7,a8+a9=﹣8,……,a99+a100=﹣99,a100+a1=﹣100,那么a1+a2+a3+……+a100的值为( )A、﹣48 B、﹣50 C、﹣98 D、﹣100二、填空题
-
11. 做生意盈亏属于正常现象,如果盈利500元记作+500元,那么-300元表示 .12. 小何买了5本笔记本,10支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小何共花费元(用含a,b的代数式表示).13. 王小毛同学做教室卫生时,发现座位很不整齐,他思考了一下,将第一座和最后一座固定之后,沿着第一座最后一座这条线就把座位摆整齐了!他利用了数学原理: .
 14. 若2xm+3y6与x5y2n为同类项,则m+n= .15. 若|a﹣2020|+|b+2021|=0,则|a+b|= .16. 一副三角板如图放置(直角顶点叠放在一起),若 , 则度.
14. 若2xm+3y6与x5y2n为同类项,则m+n= .15. 若|a﹣2020|+|b+2021|=0,则|a+b|= .16. 一副三角板如图放置(直角顶点叠放在一起),若 , 则度. 17. 如图,四个一样大的小矩形拼成一个大矩形,如果大矩形的周长为 , 那么小矩形的周长为cm.
17. 如图,四个一样大的小矩形拼成一个大矩形,如果大矩形的周长为 , 那么小矩形的周长为cm.
三、解答题
-
18. 计算:(1)、-2.3+4.3|5-8|;(2)、-32-28÷(-7)×()219. 先化简,再求值:3x2﹣3(x2﹣2x+1),其中x=1.20. 图1是由7个小正方体(每个小正方体的棱长都是1)所堆成的几何体.
 (1)、请画出这个几何体从正面、左面、上面三个方面看到的形状图;(2)、现要在这个几何体的表面上喷上油漆(不包括下底面),求需要喷上油漆的面积S21. 列方程解应用题
(1)、请画出这个几何体从正面、左面、上面三个方面看到的形状图;(2)、现要在这个几何体的表面上喷上油漆(不包括下底面),求需要喷上油漆的面积S21. 列方程解应用题欧尚超市恰好用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的与少10件,甲、乙两种商品的进价和售价如表;(注:每件商品获利=售价﹣进价).
甲
乙
进价(元/件)
20
30
售价(元/件)
25
40
(1)、该商场购进甲、乙两种商品各多少件?(2)、该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?22. 岳池县某中学为了预测本校初中毕业女生“30秒钟跳绳”项目考试情况,该校体育老师从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图所示的部分频数分布直方图(从左到右依次为第一到第六小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题: (1)、本次抽样测试的女生人数是多少人?(2)、补全频数分布直方图,第一小组所对应扇形圆心角的度数是°;(3)、若测试九年级女生“30秒钟跳绳”次数不低于90次的成绩为优秀,本校九年级女生共有280人,请估计该校九年级女生“30秒钟跳绳”成绩为优秀的人数.23. 如图,点C为线段AB上一点,点D为BC的中点,且AB=12,AC=4CD.
(1)、本次抽样测试的女生人数是多少人?(2)、补全频数分布直方图,第一小组所对应扇形圆心角的度数是°;(3)、若测试九年级女生“30秒钟跳绳”次数不低于90次的成绩为优秀,本校九年级女生共有280人,请估计该校九年级女生“30秒钟跳绳”成绩为优秀的人数.23. 如图,点C为线段AB上一点,点D为BC的中点,且AB=12,AC=4CD. (1)、求AC的长;(2)、若点E在直线AB上,且AE=3,求DE的长.24. 如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t大于0)秒.
(1)、求AC的长;(2)、若点E在直线AB上,且AE=3,求DE的长.24. 如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t大于0)秒. (1)、点C表示的数是.(2)、求当t等于多少秒时,点P到达点A处?(3)、点P表示的数是(用含字母t的式子表示)(4)、求当t等于多少秒时,P、C之间的距离为2个单位长度.25.(1)、如图1,OC是∠AOB内部的一条射线,且OD平分∠AOC,OE平分∠BOC.
(1)、点C表示的数是.(2)、求当t等于多少秒时,点P到达点A处?(3)、点P表示的数是(用含字母t的式子表示)(4)、求当t等于多少秒时,P、C之间的距离为2个单位长度.25.(1)、如图1,OC是∠AOB内部的一条射线,且OD平分∠AOC,OE平分∠BOC.
①若∠AOC=20°,∠BOC=50°,则∠EOD的度数是 ▲ .
②若∠AOC=α,∠BOC=β,求∠EOD的度数,并根据计算结果直接写出∠EOD与∠AOB之间的数量关系.
(2)、如图2,射线OC在∠AOB的外部,且OD平分∠AOC,OE平分∠BOC.试着探究∠EOD与∠AOB之间的数量关系.