广东省河源市和平县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-25 类型：期末考试

进入出卷网下载

一、单选题

1. 2022的相反数是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 截至2021年10月24日，31个省（自治区、直辖市）和新疆生产建设兵团累计报告接种新冠病毒疫苗224621.7万剂次，其中224621.7万用科学记数法表示后为（）

A、2.246217×10⁹ B、2.246217×10⁸ C、2.246217×10⁵ D、2.246217×10⁶

查看试题解析
3. 下列运算正确的是（）

A、a² - 2a²＝－a² B、3m- m＝2 C、a²b - ab²＝0 D、x-（y-x）＝-y

查看试题解析
4. 下列调查适合作抽样调查的是（）

A、了解义乌电视台“同年哥讲新闻”栏目的收视率 B、了解某甲型H1N1确诊病人同机乘客的健康状况 C、了解某班每个学生家庭电脑的数量 D、“神七”载人飞船发射前对重要零部件的检查

查看试题解析
5. 某一品牌的牛奶包装盒，该包装盒可以近似的看成是长方体，则它的展开图不可能是（）

A、 B、 C、 D、

查看试题解析
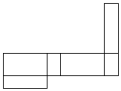6. 现定义一种新运算“*”，规定 $a * b = b^{2} - a$ ，如 $3 * 1 = 1^{2} - 3 = - 2$ ，则 $(- 2) * (- 3)$ 等于（）

A、11 B、－11 C、7 D、－7

查看试题解析
7. 若代数式2x²+3x＝8，则代数式4x²+6x+15的值是（）

A、21 B、17 C、31 D、16

查看试题解析
8. 如图是长方形窗户上的装饰物，它是由半径为 $b$ 的两个四分之一圆组成，则能射进阳光部分的面积是（）

A、 $2 a^{2} - π b^{2}$ B、 $2 a^{2} - \frac{π}{2} b^{2}$ C、 $2 a b - π b^{2}$ D、 $2 a b - \frac{π}{2} b^{2}$

查看试题解析
9. 如图，在数轴上，若点 $A ， B$ 表示的数分别是-2和10，点M到 $A ， B$ 距离相等，则M表示的数为（）

A、10 B、8 C、6 D、4

查看试题解析
10. 如图，将一副直角三角板叠放在一起，使直角顶点重合于点O，则∠COB+∠AOD=（）

A、135° B、150° C、180° D、360°

查看试题解析

二、填空题

11. 单项式 $\frac{2}{3} π r^{2} h$ 的系数是，次数是；

查看试题解析
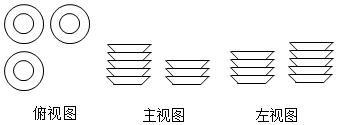
12. 计算： $3 - 3 \div (- \frac{3}{2}) \times 2$ = ．

查看试题解析
13. 在直线MN上取A、B两点，使AB＝10cm，再在线段AB上取一点C，使AC＝2cm，P、Q分别是AB、AC的中点，则PQ＝cm．

查看试题解析
14. 在一张桌子上摆放着一些碟子，从3个方向看到的3种视图如图所示，则这个桌子上的碟子共有个．

查看试题解析
15. 有理数a，b，c在数轴上的位置如图所示，若m＝|a＋b|﹣|b﹣1|﹣|a﹣c|，则m＝．

查看试题解析
16. 两村相距35千米，甲、乙两人从两村出发，相向而行，甲每小时行5千米，乙每小时行4千米，甲先出发1小时后，乙才出发，当他们相距9千米时，乙行驶了小时.

查看试题解析
17. 已知关于x的一元一次方程 $\frac{x}{2020}$ +5＝2020x+m的解为x＝2021，那么关于y的一元一次方程 $\frac{10 - y}{2020}$ ﹣5＝2020（10﹣y）﹣m的解为．

查看试题解析

三、解答题

18. 计算题： $- 1^{2021} - (\frac{2}{3} + \frac{1}{4} - \frac{5}{6}) \div (- \frac{1}{24})$ ．

查看试题解析
19. 先化简，再求值： $3 m^{2} n - [m n^{2} - \frac{1}{2} (4 m n^{2} - 6 m^{2} n) + m^{2} n] + 4 m n^{2}$ ，其中m＝－2，n＝3

查看试题解析
20. 如图，已知线段DA与B、C两点，用圆规和无刻度的直尺按下列要求画图并计算：

(1)、画直线AB、射线DC；

(2)、延长线段DA至点E，使 $A E = A B$ （保留作图痕迹）；

(3)、若AB=2cm，AD=4cm，求线段DE的长，

查看试题解析
21. 为引导学生知史爱党、知史爱国，某中学组织全校学生进行“党史知识”竞赛，该校德育处随机抽取部分学生的竞赛成绩进行统计，将成绩分为四个等级：优秀、良好、一般、不合格，并绘制成两幅不完整的统计图．
根据以上信息，解答下列问题：

(1)、德育处一共随机抽取了名学生的竞赛成绩；在扇形统计图中，表示“一般”的扇形圆心角的度数为；

(2)、将条形统计图补充完整；

(3)、该校共有1400名学生，估计该校大约有多少名学生在这次竞赛中成绩优秀？

查看试题解析
22. 某出租车沿南北方向行驶，从A地出发，晚上到达B地．规定向北为正方向．行驶记录如下（单位：㎞）：+18、-9、+7、-14、-6、+13、-6，

(1)、B地在A地的什么位置？

(2)、若出租车每行驶1㎞耗油1升，求该天共耗油多少升？

(3)、若出租车起步价为7元，起步里程为3千米（包括3千米），超过部分每千米1.2元，则该天车费多少元？

查看试题解析
23. 观察图，解答下列问题．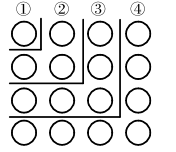

(1)、图中的圆圈被折线隔开分成六层，第一层有 $1$ 个圆圈，第二层有 $3$ 个圆圈，第三层有 $5$ 个圆圈，…，第六层有 $11$ 个圆圈．如果要你继续画下去，第 $n$ 层有个圆圈．

(2)、某一层上有 $65$ 个圆圈，这是第层．

(3)、数图中的圆圈个数可以有多种不同的方法．比如：前两层的圆圈个数和为 $(1 + 3)$ 或 $2^{2}$ ，由此得， $1 + 3 = 2^{2}$ ，同样：由前三层的圆圈个数和得： $1 + 3 + 5 = 3^{2}$ ，由前四层的圆圈个数和得： $1 + 3 + 5 + 7 = 4^{2}$ ， …根据上述规律，从 $1$ 开始的 $n$ 个连续奇数之和是多少？用 $n$ 的代数式把它表示出来

(4)、运用（3）中的规律计算： $73 + 75 + 77 + \cdot \cdot \cdot + 153$ ．

查看试题解析
24. 某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的 $\frac{1}{2}$ 多15件，甲、乙两种商品的进价和售价如下表：

甲
乙
进价（元件）
22
30
售价（元件）
29
40

(1)、该超市购进甲、乙两种商品各多少件？

(2)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？

(3)、该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品销售一部分后出现滞销，于是超市决定将剩余的乙商品五折促销，若在本次销售过程中超市共获利2350元，则以五折售出的乙商品有多少件？

查看试题解析
25. 如图，已知∠AOB＝120°，OC是∠AOB内的一条射线，且∠AOC：∠BOC＝1：2．

(1)、求∠AOC，∠BOC的度数；

(2)、作射线OM平分∠AOC，在∠BOC内作射线ON，使得∠CON：∠BON＝1：3，求∠MON的度数；

(3)、过点O作射线OD，若2∠AOD＝3∠BOD，求∠COD的度数．

查看试题解析

	甲	乙
进价（元件）	22	30
售价（元件）	29	40