广东省广州市南沙区2020-2021学年七年级上学期期末数学试题

试卷更新日期：2022-02-25 类型：期末考试

进入出卷网下载

一、单选题

1. -2的相反数是（）

A、-2 B、- $\frac{1}{2}$ C、2 D、2或-2

查看试题解析
2. 明珠湾大桥是中国（广东）自贸区南沙新区片区、广州城市副中心南沙区建设发展的重要跨江通道，是广州面向粤港澳大湾区的重大交通枢纽核心控制工程和地标性建筑．全长2233米，用科学记数法表示为（）

A、22.33×10² B、2.233×10⁴ C、2.233×10³ D、0.2233×10⁴

查看试题解析
3. 下列各组中，不是同类项的是（）

A、x³y⁴与x³z⁴ B、3x与－x C、5ab与－2ba D、－3x²y与 $\frac{1}{2} y x^{2}$

查看试题解析
4. 如图是由几个相同的小正方体搭成的一个几何体，从左边看得到的平面图形是（）

A、 B、 C、 D、

查看试题解析
5. 下列运用等式性质进行的变形，其中不正确的是（）

A、如果a＝b，那么a﹣3＝b﹣3 B、如果a＝b，那么a+ $\frac{1}{2}$ ＝b+ $\frac{1}{2}$ C、如果a＝b，那么 $\frac{a}{c} = \frac{b}{c}$ D、如果a＝b，那么ac＝bc

查看试题解析
6. 甲车间有54人，乙车间有48人，因工作的需要从乙车间调部分人去甲车间，调整后甲车间的人数是乙车间人数的2倍，若假设从乙车间调x人去甲车间，则可列方程（）

A、48＋x＝2（54﹣x） B、48＋x＝2×54 C、54﹣x＝2×48 D、54＋x＝2（48﹣x）

查看试题解析
7. 在灯塔O处观测到轮船A位于灯塔北偏西54°的方向，同时观测到轮船B位于灯塔南偏东15°的方向，那么∠AOB的大小为（）

A、131° B、141° C、151° D、159°

查看试题解析
8. 已知x﹣3y $= \frac{1}{3}$ ，则1﹣2x＋6y的值是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{5}{6}$ D、2

查看试题解析
9. 实数a、b在数轴上的位置如图所示，则下列式子成立的是（）

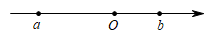A、a＋b＞0 B、﹣a＜0 C、a﹣b＜0 D、﹣a＜b

查看试题解析
10. 已知：[x]表示不大于x的最大整数．例：[3.6]＝3，[﹣0.9]＝﹣1，现定义：{x}＝x﹣[x]，例：{1.6}＝1.6﹣[1.6]＝0.6，计算{4.9}﹣{﹣1.8}的结果为（）

A、6.7 B、3.1 C、1.1 D、0.7

查看试题解析

二、填空题

11. 一个数的绝对值等于3，则这个数是.

查看试题解析
12. 若x＝﹣1是关于x的方程2x＋5a＝3的解，则a的值．

查看试题解析
13. 一个两位数，十位数字为a，个位数字为5，则这个两位数可表示为．

查看试题解析
14. 9点30分时，钟表上时针与分针所组成的角为度．

查看试题解析
15. 已知线段AB＝8cm，点D是线段AB的中点，直线AB上有一点C，并且BC＝3cm，则线段CD＝cm．

查看试题解析
16. 已知2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，2⁶＝64……则2²⁰²⁰﹣2²⁰¹⁹的个位数字是．

查看试题解析

三、解答题

17. 计算：（﹣1）¹¹﹣8÷（﹣2）＋4×|﹣5|．

查看试题解析
18. 解方程： $\frac{2 x - 1}{3} - \frac{3 x + 1}{2} = 1$

查看试题解析
19. 先化简，再求值：已知A＝3a²﹣4a，B＝4a²﹣4a﹣2，当a $= \frac{1}{2}$ 时，求A $- \frac{1}{2}$ B的值．

查看试题解析
20. 如图，点A、O、B在同一条直线上，射线OD平分∠AOC，且∠DOE＝90°．求证：OE平分∠BOC．

查看试题解析
21. 数轴上，已知AB＝a，AC＝b．令AN=2b-a，

(1)、尺规作图，在点A的左边找出点N，（保留作图痕迹，不写作法）．

(2)、若a＝5，b＝4，点A在数轴上所代表的数为﹣8，那么点N在数轴上所代表的数为多少．

查看试题解析
22. 用一批卡纸做包装盒，每张卡纸可做2个盒身或5个底盖，一个盒身与两个底盖配成一个完整的包装盒．

(1)、如果用25张卡纸做盒身，20张卡纸做底盖，做成的盒身和底盖是否正好配套？请通过计算结果加以说明．

(2)、如果有63张卡纸，请问用多少张卡纸做盒身，多少张卡纸做底盖，才能使做成的盒身和底盖正好配套？

查看试题解析
23. 某游泳场推出两种收费方式：
方式一：顾客先购买会员卡，每张会员卡100元，仅限本人一年内使用，凭卡游泳，每次游泳付费25元．
方式二：顾客不购买会员卡，每次游泳付费30元．

(1)、若某顾客一年内游泳次数为10次，请问这两种方式各收费多少元？

(2)、如何根据游泳的次数选择省钱的收费方式？通过计算验证你的看法．

查看试题解析
24. 将两块直角三角板的顶点A叠在一起，已知∠BAC＝30°，∠DAE＝90°，将三角板ADE绕点A旋转，在旋转过程中，保持∠BAC始终在∠DAE的内部．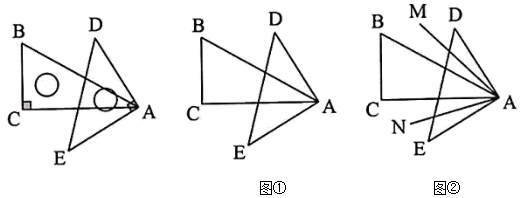

(1)、如图①，若∠BAD＝25°，求∠CAE的度数．

(2)、如图①，∠BAE与∠CAD有什么数量关系，请说明理由．

(3)、如图②，若AM平分∠BAD，AN平分∠CAE，问在旋转过程中，∠MAN的大小是否发生改变？若不变，请说明理由；若改变，请求出变化范围．

查看试题解析
25. 如图，在直角三角形ABC中，∠A＝90°，AC＝18厘米，AB＝24厘米，BC＝30厘米，点P、点Q同时从点C出发，点P以2厘米/秒的速度沿C→B→A的方向移动，点Q以1厘米/秒的速度沿C→A→B的方向移动，当点P到达点A或者点Q到达点B时，P、Q两点都停止运动，用t（秒）表示移动时间．

(1)、若点Q在边AC上时，请用含t的代数式表示线段AQ的长度．

(2)、当t为何值时，三角形BCQ的面积为144平方厘米？

(3)、若点P、Q都在AB边上运动时，是否存在P、Q两点之间的距离为12厘米？若存在，请求出t值；若不存在，请说明理由．

查看试题解析