广东省广州市番禺区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-25 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣2的相反数是（　　）

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 番禺全区常住人口为2658400人，2658400用科学记数法表示为（）

A、0.26584×10⁷ B、2.6584×10⁶ C、2.6584×10⁷ D、26.584×10⁵

查看试题解析
3. 四个有理数2、1、0、﹣1，其中最小的是（）

A、1 B、0 C、﹣1 D、2

查看试题解析
4. |﹣3|＝（）

A、3 B、﹣3 C、±3 D、0

查看试题解析
5. 多项式 $a^{2} - a + 2$ 是（）

A、二次二项式 B、二次三项式 C、三次二项式 D、三次三项式

查看试题解析
6. 下列计算正确的是（）

A、2m﹣m＝2 B、2m+n＝2mn C、2m³+3m²＝5m⁵ D、m³n﹣nm³＝0

查看试题解析
7. 以长方形的一边为轴旋转一周，得到的立体图形为（）

A、长方体 B、圆柱 C、圆锥 D、球

查看试题解析
8. 如图，OA表示北偏东20°方向的一条射线，OB表示南偏西50°方向的一条射线，则∠AOB的度数是（）

A、110° B、120° C、140° D、150°

查看试题解析
9. 运用等式性质进行的变形，不正确的是（）

A、如果a=b，那么a﹣c=b﹣c B、如果a=b，那么a+c=b+c C、如果a=b，那么ac=bc D、如果ac=bc，那么a=b

查看试题解析
10. 一商店以每件150元的价格卖出两件不同的商品，其中一件盈利25%，另一件亏损25%，则商店卖这两件商品总的盈亏情况是（）

A、亏损20元 B、盈利30元 C、亏损50元 D、不盈不亏

查看试题解析

二、填空题

11. 写出一个与﹣2x²y是同类项的单项式为．

查看试题解析
12. 45°30'＝°．

查看试题解析
13. 若x=3是关于x的方程2x+a=1的解，则a的值是．

查看试题解析
14. 如图，若∠AOB＝90°，∠COD＝90°，∠AOD＝20°，则∠BOC的大小为 °．

查看试题解析
15. 小明同学在数学实践课上，所设计的正方体盒子的平面展开图如图，每个面上都有一个汉字，请你判断，正方体盒子上与“校”字相对的面上的字是．

查看试题解析
16. 10个棱长为ycm的正方体摆放成如图的形状，则这个图形的表面积为 cm² ．

查看试题解析

三、解答题

17. 计算下列各式的值：

(1)、 $(\frac{1}{4} - \frac{1}{6} + \frac{1}{2}) \times 12$ ；

(2)、 $(- 1)^{3} \div 2 + (- \frac{1}{2})^{2} \times 8$ ．

查看试题解析
18. 解方程：

(1)、3x+7＝32﹣2x；

(2)、 $\frac{y + 1}{2} = 3 + \frac{2 - y}{4}$ ．

查看试题解析
19. 设A＝ $\frac{1}{2} x - 2 (x - \frac{2}{3} y) + (- \frac{1}{2} x + \frac{2}{3} y)$ ．

(1)、当x＝﹣2，y＝1时，求A的值；

(2)、若使求得的A的值与（1）中的结果相同，则给出的x，y的值还能够是什么？

查看试题解析
20. 测量一幢楼的高度，七次测得的数据分别是：79.8m，80.6m，80.4m，79.1m，80.3m，79.3m，80.5m．

(1)、以80为标准，用正数表示超出部分，用负数表示不足部分，写出七次测得数据对应的数；

(2)、求这七次测量的平均值；

(3)、写出最接近平均值的测量数据，并说明理由．

查看试题解析
21. 如图，平面上有四个点A，B，C，D．

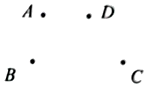(1)、依照下列语句画图：
①直线AB，CD相交于点E；
②在线段BC的延长线上取一点F，使CF＝DC．

(2)、在四边形ABCD内找一点O，使它到四边形四个顶点的距离的和OA+OB+OC+OD最小，并说出你的理由．

查看试题解析
22. 点 $A ， B ， C$ 在一条直线上， $A B = 3 c m ， B C = 1 c m$ ，求 $A C$ 的长．

查看试题解析
23. 列方程解应用题，若没有列方程，则给0分．

(1)、洗衣机厂今年计划生产洗衣机25500台，其中Ⅰ型、Ⅱ型、Ⅲ型三种洗衣机的数量比为1：2：14，计划生产这三种洗衣机各多少台？

(2)、一列火车匀速行驶，经过（从车头进人到车尾离开）一条长300m的隧道需要20s的时间．隧道的顶上有一盏灯，垂直向下发光，灯光照在火车上的时间是10s．求这列火车的长度．

查看试题解析
24. 如图所示，已知∠AOC＝2∠BOC，∠AOC的余角比∠BOC小30°．

(1)、求∠AOB的度数；

(2)、过点O作射线OD，使得∠AOC＝4∠AOD，请你求出∠COD的度数．

查看试题解析
25. 图1中，有一个平行四边形；
图2中，由2个相同的平行四边形拼成一排的图形，这图形中可以找到3个平行四边形；
图3中，由3个相同的平行四边形拼成一排的图形，这图形中可以找到6个平行四边形；
由此我们可以提出一个这样的问题：
图4中，由4个相同的平行四边形拼成一排的图形中，可以找到几个平行四边形？
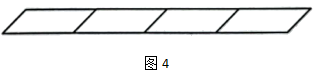
答：10个
请你根据以上事实，将一些相同的平行四边形横向或纵向拼接，由此提出一个数学问题，并写出答案．

查看试题解析