广东省潮州市潮安区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-25 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个数中，最小的数是（）

A、1 B、 $- 3$ C、 $π$ D、0

查看试题解析
2. 下列方程中，一元一次方程的是（）

A、 $2 x - 1 = 3$ B、 $x + y = 9$ C、 $\frac{2}{x} + 1 = 5$ D、 $x + 2 = x^{2}$

查看试题解析
3. 下列合并同类项正确的是（）

A、 $3 y - 2 y = 1$ B、 $- 2 x y + 4 x y = x y$ C、 $6 a b^{2} - 7 a b^{2} = - a b^{2}$ D、 $6 y^{2} + 2 y^{2} = 8 y^{4}$

查看试题解析
4. 把两块三角板按如图所示那样拼在一起，则∠ABC等于（）

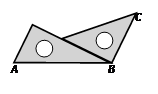A、70° B、90° C、105° D、120°

查看试题解析
5. 一个角的度数等于 $60 ° 2 0^{'}$ ，那么它的余角等于（）

A、 $40 ° 4 0^{'}$ B、 $39 ° 8 0^{'}$ C、 $119 ° 4 0^{'}$ D、 $29 ° 4 0^{'}$

查看试题解析
6. 260000000用科学记数法表示为（）

A、 $0.26 \times 1 0^{9}$ B、 $2.6 \times 1 0^{8}$ C、 $2.6 \times 1 0^{9}$ D、 $26 \times 1 0^{7}$

查看试题解析
7. 某商店以每个120元的价格卖出两个智能手表，其中一个盈利20%，另一个亏损20%．在这次买卖中，这家商店（）

A、不盈不亏 B、亏损10元 C、盈利9.6元 D、亏损9.6元

查看试题解析
8. 下列各图中，可以是一个正方体的平面展开图的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，在线段AB上有C，D两点，CD长度为1cm，AB长为整数，则以A，B，C，D为端点的所有线段长度和不可能为（）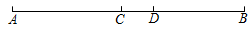

A、16cm B、21cm C、22cm D、31cm

查看试题解析
10. 观察下列三行数：
第一行：2、4、6、8、10、12……
第二行：3、5、7、9、11、13……
第三行：1、4、9、16、25、36……
设x、y、z分别为第一、第二、第三行的第100个数，则 $2 x - y + 2 z$ 的值为（）

A、9999 B、10001 C、20199 D、20001

查看试题解析

二、填空题

11. 若单项式 $5 a x^{2} y^{n + 1}$ 与 $- 7 a x^{m} y^{4}$ 的和仍是单项式，则 $m - 2 n$ ．

查看试题解析
12. 关于x的方程 $3 a - x = \frac{x}{2} + 3$ 的解是 $x = 4$ ，则 $a =$ ．

查看试题解析
13. 若小明从A处沿北偏东 $40 °$ 方向行走至点B处，又从B处沿东偏南 $20 °$ 方向行走至点C处，则 $∠ A B C =$ ．

查看试题解析
14. 一个两位数，个位上的数与十位上的数之和是12，若交换个位与十位的位置则得到的两位数为原来数字的 $\frac{4}{7}$ ，则原来的两位数是．

查看试题解析
15. 已知 $x + y = 2$ ，则 ${(x + y)}^{2} + 2 x + 2 y + 1 =$ ．

查看试题解析
16. 已知 $∠ A O B$ ，过O点作OC，若 $∠ A O C = \frac{1}{2} ∠ A O B$ ，且 $∠ A O C = 35 °$ ，则 $∠ B O C =$ ．

查看试题解析
17. 已知正整数a ， b ， c（其中a≠1）满足a^bc＝a^b+50，则a+b+c的最小值是，最大值是．

查看试题解析

三、解答题

18. 计算： $- 1^{3} - \frac{1}{4} \times (2 + {| - 3 |}^{2})$

查看试题解析
19. 先化简，再求值：
$(3 a^{2} - 3 a b + 4 b^{2}) - 2 (b^{2} + a^{2} - 2 a b + 1)$ ，其中 $a = 2$ ， $b = - 1$ ．

查看试题解析
20. 解方程： $\frac{4 x - 6}{5} + \frac{6 x - 4}{7} = - 2$

查看试题解析
21. 为鼓励居民节约用水，某市决定对居民用水收费实行“阶梯价”，具体标准如下：若每月用水量不超过18吨，按2元/吨收费；若每月用水量超过18吨，但不超过40吨，超过部分按3元/吨收费；若每月用水量超过40吨，超过部分按6元/吨收费．

(1)、若小红家某月用水30吨，则该月应交水费多少元；

(2)、若小红家某月交水费192元，求该月用水的吨数．

查看试题解析
22. 已知点B在线段AC上，点D在线段AB上．

(1)、如图1，若AB=6cm，BC=4cm，D为线段AC的中点，求线段DB的长度；

(2)、如图2，若BD= $\frac{1}{4}$ AB= $\frac{1}{3}$ CD，E为线段AB的中点，EC=12cm，求线段AC的长度．

查看试题解析
23. 某服装城共购入了两批A、B两款袜子．第一批购入A、B两款袜子共2500双，A款袜子售价为每双16元，B款袜子售价为每双24元，全部售出后的销售总额为52000元．服装城把2500双袜子全部售出后马上购入第二批袜子已知第二批袜子中，A款袜子的进货量比第一批减少了 $2 m$ 双，售价不变；B款袜子的进货量比第一批减少了 $\frac{m}{3} %$ ，售价比原售价降低了 $\frac{1}{6}$ ，两批袜子全部售出后的销售总额为94040元．

(1)、服装城第一批购入的A、B两款袜子各多少双？

(2)、该服装城第二批购进A款袜子多少双？

查看试题解析
24. 如图，已知∠AOB＝120°，射线OP从OA位置出发，以每秒2°的速度顺时针向射线OB旋转；与此同时，射线OQ以每秒6°的速度，从OB位置出发逆时针向射线OA旋转，当射线OQ达到OA后，两条射线同时停止运动．设旋转时间为t秒．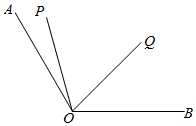

(1)、分别求出当t＝5和t＝18时，∠POQ的度数；

(2)、当OP与OQ重合时，求t的值；

(3)、当∠POQ＝40°时，求t的值．

查看试题解析
25. 小东同学在解一元一次方程时，发现这样一种特殊现象：
x+ $\frac{1}{2}$ =0的解为x=﹣ $\frac{1}{2}$ ，而﹣ $\frac{1}{2}$ = $\frac{1}{2}$ ﹣1；
2x+ $\frac{4}{3}$ =0的解为x=﹣ $\frac{2}{3}$ ，而﹣ $\frac{2}{3}$ = $\frac{4}{3}$ ﹣2．
于是，小东将这种类型的方程作如下定义：
若一个关于x的方程ax+b=0（a≠0）的解为x=b﹣a，则称之为“奇异方程”．请和小东一起进行以下探究：

(1)、若a=﹣1，有符合要求的“奇异方程”吗？若有，求出该方程的解；若没有，请说明理由；

(2)、若关于x的方程ax+b=0（a≠0）为奇异方程，解关于y的方程：a（a﹣b）y+2=（b+ $\frac{1}{2}$ ）y．

查看试题解析