安徽省合肥市巢湖市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-25 类型:期末考试
一、单选题
-
1. 下列四个有理数中是负数的是( )A、0 B、 C、2 D、3.52. 表示( )A、3个 相乘 B、3个4相乘的相反数 C、4个 相乘 D、4个3相乘的相反数3. 2021年5月11日,国家统计局权威发布第七次人口普查公报,我国最新总人口约为14.1亿人,数据“14.1亿”用科学记数法表示应为( )A、14.1×108 B、1.41×108 C、1.41×109 D、1.41×10104. 某立体图形的表面展开图如图所示,这个立体图形是( )
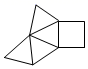 A、
A、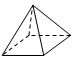 B、
B、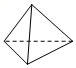 C、
C、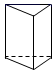 D、
D、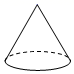 5. 若使方程 是关于 的一元一次方程,则 的值是( )A、 B、 C、 D、6. 下列不是同类项的是 ( )A、 与 B、12与 C、 与 D、 与7. 方程 去括号变形正确的是( )A、 B、 C、 D、8. 《孙子算经》是中国古代重要的数学著作,书中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有 匹,则可列方程为( )A、 B、 C、 D、9. 已知点 、 、 在一条直线上,则下列等式中,能判断 是线段 的中点的是( )A、 B、 C、 D、10. 把如图1的两张大小相同的长方形卡片放置在图2与图3中的两个相同大长方形中,已知这两个大长方形的长比宽长20cm,若记图2中阴影部分的周长为C1 , 图3中阴影部分的周长为C2 , 那么C1-C2=( )
5. 若使方程 是关于 的一元一次方程,则 的值是( )A、 B、 C、 D、6. 下列不是同类项的是 ( )A、 与 B、12与 C、 与 D、 与7. 方程 去括号变形正确的是( )A、 B、 C、 D、8. 《孙子算经》是中国古代重要的数学著作,书中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有 匹,则可列方程为( )A、 B、 C、 D、9. 已知点 、 、 在一条直线上,则下列等式中,能判断 是线段 的中点的是( )A、 B、 C、 D、10. 把如图1的两张大小相同的长方形卡片放置在图2与图3中的两个相同大长方形中,已知这两个大长方形的长比宽长20cm,若记图2中阴影部分的周长为C1 , 图3中阴影部分的周长为C2 , 那么C1-C2=( ) A、10cm B、20cm C、30cm D、40cm
A、10cm B、20cm C、30cm D、40cm二、填空题
-
11. 若一个角度数是115°6′,则这个角的补角是 .12. 若 、 互为相反数,则 的值为 .13. 幻方,最早源于我国,古人称之为纵横图.如图所示的幻方中,各行、各列以及各条对角线上的三个数字之和均相等,则图中 的值为.
 14. 把一副三角尺按如图所示拼在一起,如图,其中B,C,D三点在同一条直线上,∠ACB=45°,∠DCE=60°.
14. 把一副三角尺按如图所示拼在一起,如图,其中B,C,D三点在同一条直线上,∠ACB=45°,∠DCE=60°.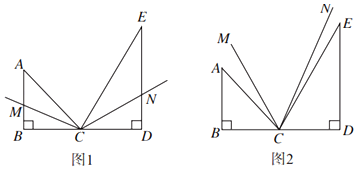 (1)、若CM和CN分别平分∠ACB和∠DCE,如图1,则∠MCN的度数为;(2)、若CM平分∠BCE,CN平分∠DCA,如图2,则∠MCN的度数为 .
(1)、若CM和CN分别平分∠ACB和∠DCE,如图1,则∠MCN的度数为;(2)、若CM平分∠BCE,CN平分∠DCA,如图2,则∠MCN的度数为 .三、解答题
-
15.16. 先化简再求值:
3(3xy – x2) −(2x2− xy),其中x=1, y=2.
17. 解方程:18. 某粮库10月23日到25日这3天内进出库的吨数记录如下(“+”表示进库,“-”表示出库):日期
10月23日
10月24日
10月25日
进出库情况
,
,
,
(1)、经过这3天进出库后,粮库管理员结算时发现粮库里结存480吨粮食,那么3天前粮库里的存量有多少吨?(2)、如果进库的装卸费是每吨8元,出库的装卸费是每吨10元,那么这3天要付出多少装卸费?19. 如图是一组有规律的图案第1个图案由4个基础图形“令”组成,第2个图案由7个基础图形组成, (1)、填表:
(1)、填表:第n个图案
1
2
3
4
n
基础图形个数
4
7
(2)、若第n个图案共有基础图形2020个,则n的值是多少?20. 现在有一种既隔热又耐老化的新型窗框材料——“断桥铝”,下图是这种材料做成的两种长方形窗框,已知窗框的长都是米,宽都是米.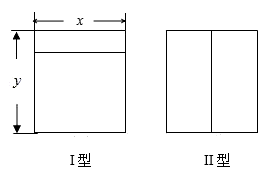 (1)、若一用户需Ⅰ型的窗框2个,Ⅱ型的窗框3个,求共需这种材料多少米(接缝忽略不计)?(2)、已知> , 求一个Ⅰ型的窗框比一个Ⅱ型的窗框节约这种材料多少米?21. 如图,点C、D是线段AB上两点,AC∶BC=3∶2,点D为AB的中点.
(1)、若一用户需Ⅰ型的窗框2个,Ⅱ型的窗框3个,求共需这种材料多少米(接缝忽略不计)?(2)、已知> , 求一个Ⅰ型的窗框比一个Ⅱ型的窗框节约这种材料多少米?21. 如图,点C、D是线段AB上两点,AC∶BC=3∶2,点D为AB的中点. (1)、如图1所示,若AB=40,求线段CD的长.(2)、如图2所示,若E为AC的中点,ED=7,求线段AB的长.22. 2017年元旦期间,某商场打出促销广告,如表所示.
(1)、如图1所示,若AB=40,求线段CD的长.(2)、如图2所示,若E为AC的中点,ED=7,求线段AB的长.22. 2017年元旦期间,某商场打出促销广告,如表所示.优惠
条件
一次性购物不超过200元
一次性购物超过200元,但不超过500元
一次性购物超过500元
优惠
办法
没有优惠
全部按九折优惠
其中500元仍按九折优惠,超过500元部分按八折优惠
小欣妈妈两次购物分别用了134元和490元.
(1)、小欣妈妈这两次购物时,所购物品的原价分别为多少?(2)、若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.23. 如图1,∠AOB是平角,∠COD是直角,射线OB在∠COD内部,OE,OF分别是∠BOD,∠AOC的平分线. (1)、如图1,若OB是∠COD的平分线,求∠AOF的度数;(2)、如图1,求∠EOF的度数;(3)、若改变∠COD的位置变化,如图2,当∠COD在直线AB的上方时,如图3,当射线OA在∠COD内部时,如图4,当∠COD在直线AB的下方时,∠EOF的度数发生变化吗?若不变,请直接写出∠EOF的度数;若不确定,请说明理由.
(1)、如图1,若OB是∠COD的平分线,求∠AOF的度数;(2)、如图1,求∠EOF的度数;(3)、若改变∠COD的位置变化,如图2,当∠COD在直线AB的上方时,如图3,当射线OA在∠COD内部时,如图4,当∠COD在直线AB的下方时,∠EOF的度数发生变化吗?若不变,请直接写出∠EOF的度数;若不确定,请说明理由.