2021-2022学年浙教版数学七下第三章整式的乘除单元检测卷

试卷更新日期：2022-02-24 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、5a-2a=3 B、a³·a⁴=a¹² C、（-a²b³）²=a⁴b⁶ D、（-a²）³=a⁶

查看试题解析
2. 计算 $3 x^{2} \cdot (- 2 x^{3})$ 的结果是（）

A、 $6 x^{5}$ B、 $- 6 x^{5}$ C、 $- 2 x^{6}$ D、 $2 x^{6}$

查看试题解析
3. 如果长方形一边长为a＋2，邻边长为2a²＋a＋1，则长方形的面积（　）

A、2a³＋5a²＋3a＋2 B、4a³＋6a²＋6a＋4 C、（2a＋4）（2a²＋a＋1） D、2a³＋2

查看试题解析
4. 下列各式中，能用平方差公式计算的是（）

A、（a+b）（﹣a﹣b） B、（a+b）（a﹣b） C、（a+b）（a﹣d） D、（a+b）（2a﹣b）

查看试题解析
5. 如图，将图1中阴影部分无重叠、无缝隙地拼成图2，根据两个图形中阴影部分的面积关系得到的等式是（）

A、a²-b²=（a+b）（a-b） B、a²+2ab+b²=（a+b）² C、a²-2ab+b²=（a-b）² D、（a+b）²-（a-b）²=4ab

查看试题解析
6. 如图的图形面积由以下哪个公式表示（）

A、a²﹣b²=a（a﹣b）+b（a﹣b） B、（a﹣b）²=a²﹣2ab+b² C、（a+b）²=a²+2ab+b² D、a²﹣b²=（a+b)（a﹣b）

查看试题解析
7. 已知一个正方形的边长为a＋1，则该正方形的面积为（）

A、a²＋2a＋1 B、a²－2a＋1 C、a²＋1 D、4a＋4

查看试题解析
8. 下列计算正确的是（）

A、 $（ 2 a + b ）^{2} = 4 a^{2} + b^{2}$ B、 $（ 5 x - 2 y ）^{2} = 25 x^{2} - 10 x y + 4 y^{2}$ C、 $（ \frac{1}{2} x - y ）^{2} = \frac{1}{2} x^{2} - x y + y^{2}$ D、 $（ \frac{1}{2} x + \frac{1}{3} ）^{2} = \frac{1}{4} x^{2} + \frac{1}{3} x + \frac{1}{9}$

查看试题解析
9. 2021年9月15日消息，钟南山等团队首次精确描绘德尔塔病毒传播链，该研究揭示了德尔塔变异毒株具有潜伏期短、传播速度快、病毒载量高、核酸转阴时间长、更易发展为危重症等特点．德尔塔病毒的直径约为0.00000008m，数字0.00000008用科学记数法表示为（）

A、 $8 \times 1 0^{- 8}$ B、 $0.8 \times 1 0^{- 8}$ C、 $0.8 \times 1 0^{- 7}$ D、 $8 \times 1 0^{- 7}$

查看试题解析
10. 下列运算正确的是（）

A、 $3 a + 2 a = 5 a^{2}$ B、 $- 8 a^{2} \div 4 a = 2 a$ C、 ${(- 2 a^{2})}^{3} = - 8 a^{6}$ D、 $4 a^{3} \cdot 3 a^{2} = 12 a^{2}$

查看试题解析

二、填空题

11. 如果多项式6x²-kx-2因式分解后有一个因式为3x-2，则k= ．

查看试题解析
12. 将代数式 $\frac{y^{- 2}}{5 x^{- 1}}$ 化为只含有正整数指数幂的形式

查看试题解析
13. 计算：
（b+12）（）=b²-144.
()（- $\frac{1}{3}$ x+0.5y）= $\frac{1}{9}$ x²- $\frac{1}{4}$ y².

查看试题解析
14. 写出 $\sqrt{a} - \sqrt{b} (a \geq 0 ， b \geq 0)$ 的一个有理化因式是．

查看试题解析
15. 若 $x^{2} + a x + b = (x + 3) (x - 4) ，则 a$ = ， b=

查看试题解析
16. 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为 $S_{1}$ ；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为 $S_{2}$ .若 $a + b = 8 ， a b = 10$ ，则 $S_{1}$ ＋ $S_{2}$ ＝；当 $S_{1}$ ＋ $S_{2}$ ＝40时，则图3中阴影部分的面积 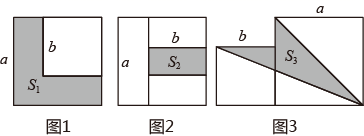$S_{3} =$ .

查看试题解析

三、解答题

17. 已知m²＋ $\frac{1}{m^{2}}$ ＝4，求m＋ $\frac{1}{m}$ 和m－ $\frac{1}{m}$ 的值．

查看试题解析
18. 若无理数A的整数部分是a，则它的小数部分可表示为A-a．例如：π的整数部分是3，因此其小数部分可表示为π-3．若x表示 $\sqrt{47}$ 的整数部分，y表示它的小数部分，求代数式( $\sqrt{47}$ +x)y的值．

查看试题解析
19. 已知 $a = \frac{1}{2014} x + 2013$ ， $b = \frac{1}{2014} x + 2014$ ， $c = \frac{1}{2014} x + 2015$ ，求代数式 $2 (a^{2} + b^{2} + c^{2} - a b - b c - a c)$ 的值.

查看试题解析
20. 阅读理解：
已知a+b=-4，ab=3，求a²+b²的值。

解：∵a+b=-4，

$∴$ （a+b）²=（-4）² ，

即a²+2ab+b²=16.

∵ab=3，

∴a²+b²=10

参考上述过程解答问题.

(1)、已知a-b=-3，ab=-2，求（a-b）（a²+b²）的值；

(2)、若m-n-p=-10，（m-p）n=-12，求（m-p）²+n²的值.

查看试题解析
21. 一个宽为a、长为4b的长方形如图1所示，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）。

(1)、观察图2，请你用等式表示（a+b）² ，（a-b）² ，
ab之间的数量关系：。

(2)、根据（1）中的结论，如果x+y=5，xy= $\frac{9}{4}$ ，求代数式（x-y）²的值。

(3)、如果（2019-m）²+（m-2020）²=7。
求（2019-m）（m-2020）的值。

查看试题解析
22. 乘法公式的探究及应用.

(1)、如图1，可以求出阴影部分的面积是（写成两数平方差的形式）；

(2)、如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是，长是，面积是（写成多项式乘法的形式）；

(3)、比较以上两图的阴影部分面积，可以得到乘法公式：（用式子表达）；

(4)、运用你所得到的公式，计算下列式子.
①1002×998
②（2+1）（2²+1）（2⁴+1）…（2³²+1）+1.

查看试题解析
23.

(1)、如图1所示，若大正方形的边长为 $a$ ，小正方形的边长为 $b$ ，则阴影部分的面积是；若将图1中的阴影部分裁剪下来，重新拼成如图2所示的一个长方形，则它的面积是；

(2)、由（1）可以得到一个乘法公式是；

(3)、利用你得到的公式计算： $202 1^{2} - 2022 \times 2020$ ．

查看试题解析
24. 探究下面的问题：

(1)、如图甲，在边长为a的正方形中去掉一个边长为b的小正方形（a＞b），把余下的部分剪拼成如图乙的一个长方形，通过计算两个图形（阴影部分）的面积，验证了一个等式，这个等式是（用式子表示），即乘法公式中的公式．

(2)、运用你所得到的公式计算：
①10.3×9.7；
②（x+2y﹣3z）（x﹣2y﹣3z）．

查看试题解析

2021-2022学年浙教版数学七下第三章整式的乘除 单元检测卷

一、单选题

二、填空题

三、解答题

2021-2022学年浙教版数学七下第三章整式的乘除单元检测卷