初中数学北师大版八年级下册第二章 一元一次不等式(组)全章测试
试卷更新日期:2022-02-24 类型:单元试卷
一、单选题
-
1. 据天气预报2018年4月12日大田县的最高气温是32℃,最低气温是21℃,则当天大田县气温t(℃)的变化范围是( )A、t>21 B、t<32 C、21<t<32 D、21≤t≤322. 下列说法正确的是( )A、若a<b,则3a<2b B、若a>b,则ac2>bc2 C、若﹣2a>2b,则a<b D、若ac2<bc2 , 则a<b3. 不等式组的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若不等式(a+1)x>2的解集为x< ,则a的取值范围是( )A、a<1 B、a<-1 C、a>1 D、a>-15. 已知直角坐标系中,点 在第四象限,则x的取值范围( )A、 B、 C、 D、6. 某校在一次外出郊游中,把学生编为9个组,若每组比预定的人数多1人,则学生总数超过200人;若每组比预定的人数少1人,则学生总数不到190人,那么每组预定的学生人数为( )A、24人 B、23人 C、22人 D、不能确定7. 一次函数y=mx﹣n(m,n为常数)的图象如图所示,则不等式mx﹣n≥0的解集是( )
4. 若不等式(a+1)x>2的解集为x< ,则a的取值范围是( )A、a<1 B、a<-1 C、a>1 D、a>-15. 已知直角坐标系中,点 在第四象限,则x的取值范围( )A、 B、 C、 D、6. 某校在一次外出郊游中,把学生编为9个组,若每组比预定的人数多1人,则学生总数超过200人;若每组比预定的人数少1人,则学生总数不到190人,那么每组预定的学生人数为( )A、24人 B、23人 C、22人 D、不能确定7. 一次函数y=mx﹣n(m,n为常数)的图象如图所示,则不等式mx﹣n≥0的解集是( )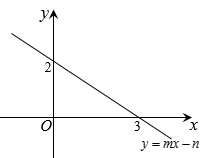 A、x≥2 B、x≤2 C、x≥3 D、x≤38. 已知关于 的不等式组 有且只有两个整数解,则 的取值范围是( )A、 B、 C、 D、
A、x≥2 B、x≤2 C、x≥3 D、x≤38. 已知关于 的不等式组 有且只有两个整数解,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
9. 不等式 的解集是.10. 已知一次函数y=ax+b(a、b是常数),x与y的部分对应值如下表:不等式ax+b>0的解集是 .
x
-2
-1
0
1
2
3
y
6
4
2
0
-2
-4
11. 若 ,则 (用“<”或“>”填空)12. 定义新运算:对于任意实数a,b都有:a⊕b=a(a﹣b)+1.如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式﹣3⊕x<15的解为 .13. 去年绵阳市空气质量良好(二级以上)的天数与全年天数(365)之比达到80%,如果明年(365天)这样的比值要超过90%,那么明年空气质量良好的天数比去年至少要增加天.14. 关于x的不等式的解集是 , 则关于x的不等式的解集是 .15. 经历了漫长艰难的体训,初三学子即将迎来中考体考,初三某班的家长为孩子们准备了脉动饮料、士力架和葡萄糖口服液.已知脉动饮料、士力架和葡萄糖口服液的单价之和为22元,计划购买脉动饮料、士力架和葡萄糖口服液的数量总共不超过200,其中葡萄糖口服液的单价为10元,计划购买50支.脉动饮料的数量不多于士力架数量的一半,但至少购买30瓶.在做预算时,将脉动饮料和士力架的单价弄反了,结果在实际购买时,总费用比预算多了160元.若脉动饮料、士力架和葡萄糖口服液的单价均为整数,则实际购买脉动饮料、士力架和葡萄糖口服液的总费用最多需要花费元.16. 已知关于x、y的方程组 的解都为非负数,且满足 , ,若 ,则z的取值范围是三、计算题
-
17. 解不等式.
四、解答题
-
18. 解不等式组: 并把解集在数轴上表示出来.
 19. 已知a,b,c是△ABC的三边长,若b=2a﹣1,c=a+5,且△ABC的周长不超过20cm,求a的范围.20. 某地为引导旅客来旅游及消费,计划5月至9月开展全城推广活动.某旅行社为吸引市民组团去旅游,推出了如下收费标准:如果人数不超过25人,人均旅游费用为2000元;如果超过25人,每增加1人,人均旅游费用降低40元,但人均旅游费用不得低于1700元.某单位组织员工去旅游,共支付给该旅行社旅游费用54000元,请问该单位这次共有多少员工去旅游?
19. 已知a,b,c是△ABC的三边长,若b=2a﹣1,c=a+5,且△ABC的周长不超过20cm,求a的范围.20. 某地为引导旅客来旅游及消费,计划5月至9月开展全城推广活动.某旅行社为吸引市民组团去旅游,推出了如下收费标准:如果人数不超过25人,人均旅游费用为2000元;如果超过25人,每增加1人,人均旅游费用降低40元,但人均旅游费用不得低于1700元.某单位组织员工去旅游,共支付给该旅行社旅游费用54000元,请问该单位这次共有多少员工去旅游?五、综合题
-
21. 某校九年级有三个班,其中九年一班和九年二班共有105名学生,在期末体育测试中,这两个班级共有79名学生满分,其中九年一班的满分率为70%,九年二班的满分率为80%.(1)、求九年一班和九年二班各有多少名学生.(2)、该校九年三班有45名学生,若九年级体育成绩的总满分率超过75%,求九年三班至少有多少名学生体育成绩是满分.22. 经销商销售甲型、乙型两种产品,价格随销售量的变化而不同,具体如表:
销售量(件
价格(元件)
型号
甲型
乙型
已知销售10件甲型产品和30件乙型产品的销售额为750元;销售60件甲型产品和100件乙型产品的销售额为2520元.
(1)、求、的值;(2)、若学校要购买甲型、乙型两种产品共101件,购买的甲产品少于乙产品,所用经费不超过1680元,则有多少种购买方案?23. 在平面直角坐标系中,直线 与 轴交于点 ,直线 与 轴交于点 ,与直线 交于点 ,设点 的横坐标为-2. (1)、求点 的坐标及 的值;(2)、根据图象直接写出不等式 的解集;(3)、点 为 轴上一点,当 最大时,求点 的坐标.24. 瑞安市高楼绿道有二人座,三人座,四人座三种规格的共享单车供游客租赁,其收费标准如下表:
(1)、求点 的坐标及 的值;(2)、根据图象直接写出不等式 的解集;(3)、点 为 轴上一点,当 最大时,求点 的坐标.24. 瑞安市高楼绿道有二人座,三人座,四人座三种规格的共享单车供游客租赁,其收费标准如下表:车型 二人座 三人座 四人座 价格(元/小时) 20 40 60 某单位组织员工到该景点春游,共租赁n辆这三种共享单车,且三人座共享单车是二人座共享单车数量的2倍。
(1)、当n=20时,①若该单位有60人,租赁的每辆车都坐满人,则租赁了多少辆三人座的共享单车?
②请设计一个租金金额最少的方案,并求出租金金额;
(2)、若该单位主管打算用于租这三种共享单车的总资金为2080元,则最多能租多少辆共享单车供员工使用?25. 对 , 定义一种新运算 (中 , 均为非零常数).例如: ;已知 , .(1)、求 , 的值;(2)、若关于 的不等式组 恰好只有 个整数解,求 的取值范围.
-