2021-2022学年浙教版数学七下3.5 整式的化简同步练习

试卷更新日期：2022-02-24 类型：同步测试

进入出卷网下载

一、单选题

1. 比较a²+b²与2ab的大小，叙述正确的是（）

A、a²+b²≥2ab B、a²+b²>2ab C、由a的大小确定 D、由b的大小确定

查看试题解析
2. 计算（x+3y）²-（3x+y）²的结果是（）

A、8x²-8y² B、8y²-8x² C、8（x+y）² D、8（x-y）²

查看试题解析
3. 已知（12a³-6a²+3a）÷（3a）-2a=0且b=2，则式子（ $\frac{2}{3}$ ab²-2ab）· $\frac{1}{2}$ ab的值为（）.

A、- $\frac{1}{3}$ B、 $\frac{1}{2}$ C、-1 D、2

查看试题解析
4. 若（ax-y）²=4x²-4xy+by² ，则a，b的值分别为（）

A、a=2，b=1 B、a=-2，b=1 C、a=-2，b=-1 D、a=4，b=1

查看试题解析
5. 当x=- $\frac{7}{12}$ 时，代数式（x-2）²-2（2-2x）-（1+x）（1-x）的值等于（）

A、- $\frac{23}{72}$ B、 $\frac{23}{72}$ C、1 D、 $\frac{49}{72}$

查看试题解析
6. 如果x²+x=3，那么代数式（x+1）（x-1）+x（x+2）的值是（）

A、2 B、3 C、5 D、6

查看试题解析
7. 下列各式中，能用完全平方公式计算的是（）

A、（3a-2b）（-2b-3a） B、（3a+2b）（-3a-2b） C、（3a+2b）（-2a-3b） D、（3a-2b）（3a+2b）

查看试题解析
8. 若 $x + y = 6$ ， $x^{2} + y^{2} = 20$ ，求 $x y$ 的值是（）

A、6 B、8 C、26 D、20

查看试题解析
9. 如图，四个全等的直角三角形和中间的小正方形可以拼成一个大正方形，若直角三角形的较长直角边长为a，较短直角边长为b，大正方形面积为S₁ ，小正方形面积为S₂ ，则（a+b）²可以表示为（）

A、S₁﹣S₂ B、S₁+S₂ C、2S₁﹣S₂ D、S₁+2S₂

查看试题解析
10. 多项式x²+A+1是个完全平方式，那么代数式A不可能为（）

A、2x B、x C、﹣2x D、 $\frac{1}{4}$ x⁴

查看试题解析

二、填空题

11. 如图，任意输入一个非零数，则输出的数是.

查看试题解析
12. 已知（x-1）²=2，则代数式2x²-4x+5=.

查看试题解析
13. 已知x²-y²=6，且x=2-y，则x-y=.

查看试题解析
14. 当x=7时，代数式（2x+5）（x+1）-（x-3）（x+1）的值为.

查看试题解析
15. 若 $x^{2} y + x y^{2} = 30$ ， $x y = 6$ ，则 $x - y$ 的值为．

查看试题解析
16. 现有甲、乙、丙三种不同的正方形或长方形纸片若干张（边长如图）．要用这三种纸片无重合无缝隙拼接成一个大正方形，先取甲纸片1张，乙纸片4张，还需取丙纸片张．

查看试题解析

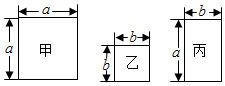
三、解答题

17. 若（x^m÷^x2n）³÷x2^m-n与2x³是同类项，且m+5n=13，求m²-25n的值.

查看试题解析
18. 先化简，再求值.
（2x-y）¹³÷[（2x-y）³]²÷[（y-2x）²]³ ，其中x=2，y=-1.

查看试题解析
19. 先化简，再求值：（2a-3b）（3a+2b）-（2a+b）·（a-2b），其中a=-1，b=-1.

查看试题解析
20. 设 $x_{1}$ ， $x_{2}$ 是关于x的一元二次方程 $x^{2} - 2 (m + 1) x + m^{2} + 3 = 0$ 的两个实数根.

(1)、求m的取值范围；

(2)、若 $x_{1}^{2} + x_{2}^{2} = | x_{1} | + | x_{2} | + x_{1} x_{2}$ ，求m的值.

查看试题解析
21. 已知A=（4x⁴-x²）÷x² ， B=（2x+5）（2x-5）+1.

(1)、求A和B；

(2)、若变量y满足y-A=B，求y与x的关系式；

(3)、在（2）的条件下，当y=7时，求8x²+（8x²-y）²-30的值.

查看试题解析
22. 化简求值.

(1)、已知a²+a-3=0，求a²（a+4）的值；

(2)、已知a²+7a=-6，求（3a-2）（a-3）-（2a-1）²的值；

(3)、已知x-2y=-3，求（x+2）²-6x+4y（y-x+1）的值.

查看试题解析
23. 如图所示，在某一禁毒基地的建设中，准备在一个长为（6a+5b）米，宽为（5b-a）米的长方形草坪上修建两条宽为a米的通道.

(1)、求剩余草坪的面积是多少平方米？

(2)、若a=1，b=3，求剩余草坪的面积是多少平方米.

查看试题解析
24. 两个边长分别为a和b的正方形如图1所示，其中未叠合部分（阴影）面积为S₁；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为S_2..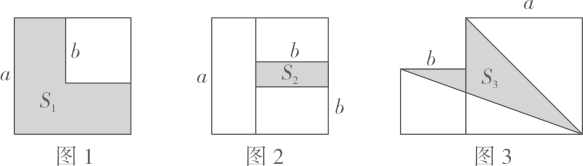

(1)、用含a，b的代数式分别表示S₁ ， S₂；

(2)、若a+b=10，ab=22，求S₁+S₂的值；

(3)、当S₁+S₂=32时，求出图3中阴影部分的面积S_3.

查看试题解析