四川省宜宾市2021-2022学年八年级上学期期末数学试卷

试卷更新日期：2022-02-24 类型：期末考试

进入出卷网下载

一、单选题

1. 16的平方根是（）

A、 4 B、±4 C、±2 D、±8

查看试题解析
2. 下列运算正确的是（）

A、a²+a⁴＝a⁶ B、（a²）³＝a⁸ C、（3a²b³）²＝9a⁴b⁶ D、a⁸÷a²＝a⁴

查看试题解析
3. 某学校对八年级1班50名学生进行体能评定，进行了“长跑”、“立定跳远”、“跳高”的测试，根据测试总成绩划分体能等级，等级分为“优秀”、“良好”、“合格”、“较差”四个等级，该班级“优秀”的有28人，“良好”的有15人，“合格”的有5人，则该班级学生这次体能评定为“较差”的频率是（）

A、2 B、0.02 C、4 D、0.04

查看试题解析
4. 如图，OD平分∠AOB，点P是OD上一点，PE⊥OA于E，且PE＝3，点N是OB上的点，则线段PN的取值范围是（）

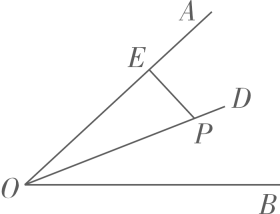A、PN≥3 B、PN＞3 C、PN≤3 D、PN＜3

查看试题解析
5. 如图所示，已知数轴上的点A、O、B、C、D分别表示数﹣2、0、1、2、3，则表示数3 $- \sqrt{5}$ 的点P应落在（）

A、线段AO上 B、线段OB上 C、线段BC上 D、线段CD上

查看试题解析
6. 已知△ABC中，∠A、∠B、∠C所对的边分别是a、b、c，满足下列条件的三角形中，不能判定△ABC为直角三角形是的（）

A、∠A：∠B：∠C＝3：4：5 B、∠A＝∠C﹣∠B C、a：b：c＝5：12：13 D、∠A：∠B：∠C＝1：2：3

查看试题解析
7. 下列各式从左到右的变形中，是因式分解且完全正确的是（）

A、（x+2）（x﹣2）＝x²﹣4 B、x²﹣2x﹣3＝x（x﹣2）﹣3 C、x²﹣4x+4＝（x﹣2）² D、x³﹣x＝x（x²﹣1）

查看试题解析
8. 下列命题是真命题的是（）

A、两直线平行，同旁内角相等 B、有一个角是60°的三角形是等边三角形 C、有两条边和一个角对应相等的两个三角形一定全等 D、到一条线段的两端距离相等的点，必在这条线段的垂直平分线上

查看试题解析
9. 如图，三条笔直的公路两两相交，交点分别在点A、B、C处，有两户村民分别在点D和点E处，现准备建造一个蓄水池，要求水池到两条公路AB、BC的距离相等，且到两户村民D、E的距离相等，则水池修建的位置应该是（）

A、在∠B的平分线与DE的交点处 B、在线段AB、AC的垂直平分线的交点处 C、在∠B的平分线与DE的垂直平分线的交点处 D、在∠A的平分线与DE的垂直平分线的交点处

查看试题解析
10. 如图，Rt $△$ ABC中，∠ACB＝90°，AC＝BC，过点C在 $△$ ABC外作直线DE，分别过点A、B作DE的垂线，垂足分别为E、D，若AE＝4，BD＝3，则DE之长为（）

A、5 B、7 C、8 D、12

查看试题解析
11. 如图所示，将如图一所示的大小相同的四个小正方形按图二所示的方式放置在一个边长为a的大正方形中，中间恰好空出两条互相垂直的宽都为b的长方形，根据图二中阴影部分的面积计算方法可以验证的公式为（）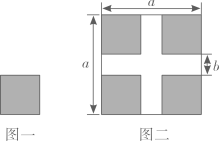

A、（a+b）（a﹣b）＝a²﹣b² B、（a+b）²＝a²+2ab+b² C、（a﹣b）²＝a²﹣2ab+b² D、（a﹣b）²＝（a+b）²﹣4ab

查看试题解析
12. 已知Rt $△$ ABC中，∠ACB＝90°，AC＝BC，AB＝4 $\sqrt{2}$ ，D为BC的中点，E是线段AB上一点，连接CE、DE，则CE+DE的最小值是（）

A、2 $\sqrt{3}$ B、2 $\sqrt{5}$ C、4 $\sqrt{2}$ D、2+2 $\sqrt{2}$

查看试题解析

二、填空题

13. 若一个数的立方根是﹣3，则这个数是.

查看试题解析
14. 分解因式：x³﹣25x＝.

查看试题解析
15. 化简：（8x³y³﹣4x²y²）÷2xy²＝.

查看试题解析
16. 已知2^x＝a，则2^x•4^x•8^x＝（用含a的代数式表示）.

查看试题解析
17. 如图所示的长方体中，长AB＝5cm，宽BC＝3cm，高CD＝6cm，一只蚂蚁从顶点A处沿长方体的表面爬行到点D处，它爬行的最短距离为.

查看试题解析
18. 已知：Rt $△$ ABC中，∠BAC＝90°，AB＝AC＝1，D是BC边上的一个动点（其中0°＜∠BAD＜45°），以AD为直角边作Rt $△$ ADE，其中∠DAE＝90°，且AD＝AE，DE交AC于点F，过点A作AH⊥DE于点G，交BC于H，在D点的运动过程中，有下列结论：① $△$ ABD≌ $△$ ACE：②BD²+DC²＝2AD²；③BD²+HC²＝DH²；④当BD $= \sqrt{2} -$ 1时，AC平分∠HAE；⑤当∠BAD＝22.5°时， $S_{△ A D G} = 2 S_{△ A G F}$ ，其中正确的有 .（将所有正确结论的番号填在答题卡对应题号的横线上）

查看试题解析

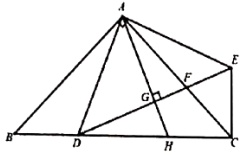
三、解答题

19. 计算或因式分解：

(1)、计算： ${(- 3)}^{2} + \sqrt[3]{8} - \sqrt{16} \div (- \frac{2}{3}) + {(- 1)}^{2021}$ ；

(2)、因式分解： $x (x - 6) + 9$ ；

(3)、化简： $2 x (x - 1) - (x + 1) (x - 1) + {(x + 1)}^{2}$ .

查看试题解析
20. 已知 $\sqrt{a + b - 3} +$ （ab﹣4）²＝0.求代数式a²+b²的值.

查看试题解析
21. 某中学为推动学生“海量阅读”，准备添加一批书籍，为了了解学生阅读的喜好，使添加的书籍更切合学生的需求，在全校学生中随机抽取部分学生进行问卷调查，调查要求每人只选取一种最喜爱的书籍，如果没有喜爱的书籍，则作“其他”类统计，将收集的数据绘制成图一、图二两幅不完整的统计图.

(1)、求参与这次问卷调查的学生人数；

(2)、补全图一中小说和科普的图形；

(3)、求图二中，“小说”所在扇形的圆心角的度数.

查看试题解析
22. 已知：Rt $△$ ABC中，∠B＝90°，D是BC上一点，DF⊥BC交AC于点H，且DF＝BC，FG⊥AC交BC于点E.求证：AB＝DE.

查看试题解析
23. 仔细阅读下面例题，解答问题：
观察下列各计算题：

26×682＝286×62

34×473＝374×43

52×275＝572×25

15×561＝165×51

……

以上每个等式都非常巧妙，左边是一个两位数乘以三位数，等式两边的数字之间具有特殊性，一边的数字也有特殊性，且数字关于等号成对称分布，我们把满足这种条件的等式称为“对称积等式”.

(1)、解决问题：填空，使下列各式成为“对称积等式”：41×154＝×14； ×286＝682×

(2)、解决问题：设“对称积等式”这类等式左边两位数的十位数字为a，个位数字为b，
①写出a+b的取值范围；

②请用含a、b的代数式写出表示“对称积等式”的式子，并证明你的结论.

查看试题解析
24. 如图，已知长方形的边AD＝8，AB＝4，动点M从点A出发，以每秒2个单位长度的速度沿A→D→A的路径匀速运动，同时，动点N从点C出发，沿C→B方向以每秒1个单位长度的速度匀速运动，当其中一个动点到达终点时，另一点也随之停止运动，设运动时间为t秒.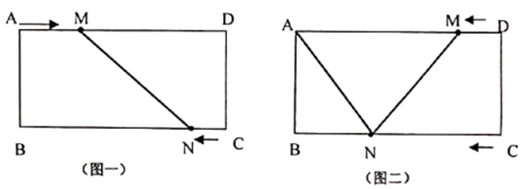

(1)、如（图一），当运动时间为1秒时，求MN的长度；

(2)、当0≤t≤4时，直接写出 $△$ AMN为直角三角形时的运动时间t的值；

(3)、如（图二），当4＜t＜8时，判断 $△$ AMN的形状，并说明理由.

查看试题解析
25.

(1)、如（图一），分别以 $△$ ABC的两边AB、AC为直角边向外作两个等腰直角三角形，∠EAB＝∠DAC＝90°，AE＝AB，AD＝AC，连接BD、CE交于点F.
①求证：BD＝CE；

②当BC和AC满足什么数量关系时，点F是BD的中点，并说明理由；

(2)、运用（1）解答中获取的经验，解决问题：如（图二），为了测量一狭长水库两端A、B的距离，小王在水库旁边的空地上选择点C，能直达点A和点B，并以AC为斜边在 $△$ ABC内作Rt $△$ ACD，且DA＝DC，连接BD：测得∠DBC＝15°，DB＝1千米，BC $= \sqrt{2}$ 千米，请根据测量结果直接写出AB之长（结果保留根号）

查看试题解析