四川省凉山彝族自治州2021-2022学年八年级上学期期末数学试卷

试卷更新日期：2022-02-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 王师傅用4根木条钉成一个四边形木架，如图，要使这个木架不变形，他至少还要再钉上几根木条？（）

A、0根 B、1根 C、2根 D、3根

查看试题解析
3. 如图，已知△ABE≌△ACD，∠1=∠2，∠B=∠C，不正确的等式是（）

A、AB=AC B、∠BAE=∠CAD C、BE=DC D、AD=DE

查看试题解析
4. 下列计算正确的是（）

A、2a+3b=5ab B、（x+2）²=x²+4 C、（ab³）²=ab⁶ D、（﹣1）⁰=1

查看试题解析
5. 如图，给出了正方形ABCD的面积的四个表达式，其中错误的是（）

A、 $(x - a) (x - a)$ B、 $x^{2} + a^{2} + 2 a x$ C、 $(x + a) (x + a)$ D、 $(x + a) a + x (x + a)$

查看试题解析
6. 三角形中，最大角 $α$ 的取值范围是（）

A、 $0 ° < α < 90 °$ B、 $60 ° < α < 180 °$ C、 $60 ° \leq α < 90 °$ D、 $60 ° \leq α < 180 °$

查看试题解析
7. 如图所示，BO，CO分别是∠ABC，∠ACB的两条角平分线，∠A=100°，则∠BOC的度数为（）．

A、80° B、90° C、120° D、140°

查看试题解析
8. 若 $(x - 3) (x + 5) = x^{2} + p x + q$ ，则 $p$ 为（）

A、－15 B、2 C、8 D、－2

查看试题解析
9. 如图， $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 + ∠ 5 + ∠ 6 =$ （）度.

A、180 B、270 C、360 D、540

查看试题解析
10. 若把分式 $\frac{3 a b}{2 a + b}$ 中的a、b都缩小为原来的 $\frac{1}{3}$ ，则分式的值（）

A、缩小为原来的 $\frac{1}{3}$ B、扩大为原来的6倍 C、缩小为原来的 $\frac{1}{9}$ D、不变

查看试题解析
11. $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1) + 1$ 的计算结果是（）

A、 $3^{32} + 1$ B、 $3^{32} - 1$ C、 $3^{31}$ D、 $3^{32}$

查看试题解析
12. 已知关于 $x$ 的分式方程 $\frac{x - 2}{x + 2} - \frac{m x}{x^{2} - 4} = 1$ 无解，则 $m$ 的值为（）

A、0 B、0或－8 C、－8 D、0或－8或－4

查看试题解析
13. 已知：在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ 交BC于D，若 $B C = 36$ ，且 $B D ： D C = 8 ： 4$ ，则点D到AB边的距离为（）

A、18 B、12 C、14 D、16

查看试题解析
14. 将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为（）

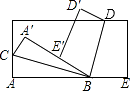A、60° B、75° C、90° D、95°

查看试题解析
15. 如图， $△ M N P$ 中， $∠ P = 60 °$ ， $M N = N P$ ， $M Q ⊥ P N$ ，垂足为Q，延长MN至G，取 $N G = N Q$ ，若 $△ M N P$ 的周长为12， $M Q = m$ ，则 $△ M G Q$ 周长是（）

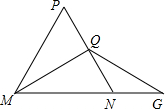A、8＋2m B、8＋m C、6＋2m D、6＋m

查看试题解析

二、填空题

16. 某种细胞的平均半径是0.0036m，用科学记数法可表示为m.

查看试题解析
17. 在实数范围内分解因式： $a^{4} - 4 =$ ．

查看试题解析
18. 二次三项式 $x^{2} - k x + 9$ 是一个完全平方式，则k=.

查看试题解析
19. 已知点M（x,3）与点N（－2，y）关于x轴对称，则3x+2y= ．

查看试题解析
20. 如图，小华从点A出发向前走10m，向右转15°，然后继续向前走10m，再向右转15°，他以同样的方法继续走下去，当他第一次回到点A时共走了m.

查看试题解析
21. 如图，在△ABC中，AB＝AC＝24厘米，∠B=∠C ，BC＝16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为厘米/秒时，能够在某一时刻使△BPD与△CQP全等．

查看试题解析

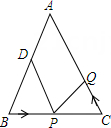
三、解答题

22.

(1)、计算： ${(- 2 a^{2} b)}^{3} - 8 {(a^{2})}^{2} \cdot {(- a)}^{2} \cdot {(- b)}^{3}$ ；

(2)、已知 $a^{2} - a - 1 = 0$ ，求代数式 $(1 - \frac{1}{a + 1}) \div \frac{a^{3}}{a^{2} + 2 a + 1}$ 的值.

(3)、先化简，再求值：
$(9 x^{3} y - 12 x y^{3} + 3 x y^{2}) \div (- 3 x y) - (2 y + x) (2 y - x)$ ，其中 $x = 1$ ， $y = - 2$ .

查看试题解析
23. 先化简，再求值： $(\frac{1}{x^{2} - 2 x} - \frac{1}{x}) \div \frac{x - 3}{x^{2} - 4}$ ，其中 $- 1 < x < 4$ ，且 $x$ 为整数.

查看试题解析
24. 如图，在所给正方形网格图中完成下列各题：

(1)、画出格点△ABC（顶点均在格点上）关于直线DE对称的△A₁B₁C₁ ；

(2)、在DE上画出点Q，使△QAB的周长最小.

查看试题解析
25. 如图， $C E = D E$ ， $A E = B E$ ， $∠ 1 = ∠ 2$ ，点D在 $A C$ 边上， $A E$ 和 $B D$ 相交于点O ．

(1)、求证： $△ A E C ≌ △ B E D$ ；

(2)、若 $∠ 1 = 42 °$ ，求 $∠ 3$ 的度数．

查看试题解析
26. 某商店计划今年的圣诞节购进A、B两种纪念品若干件．若花费480元购进的A种纪念品的数量是花费480元购进B种纪念品的数量的 $\frac{3}{4}$ ，已知每件A种纪念品比每件B种纪念品多4元．

(1)、求购买一件A种纪念品、一件B种纪念品各需多少元？

(2)、若商店一次性购买A、B纪念品共200件，要使总费用不超过3000元，最少要购买多少件B种纪念品？

查看试题解析
27. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，直线 $M N$ 经过点 $C$ ，且 $A D ⊥ M N$ 于 $D$ ， $B E ⊥ M N$ 于 $E$ .

(1)、当直线 $M N$ 绕点 $C$ 旋转到图1的位置时，

①求证： $△ A D C$ ≌ $△ C E B$ ；

②求证： $D E = A D + B E$ ；

(2)、当直线 $M N$ 绕点 $C$ 旋转到图2的位置时，（1）中的结论②还成立吗？若成立，请给出证明；若不成立，说明理由.

查看试题解析