江苏省镇江市句容市2021-2022学年八年级上册数学期末学情检测试卷

试卷更新日期：2022-02-24 类型：期末考试

进入出卷网下载

一、填空题

1. 4的平方根是

查看试题解析
2. 小亮的体重为 $49.65 kg$ ，精确到 $0.1 kg$ 得到的近似值为 $kg$ .

查看试题解析
3. 若一次函数y＝2x﹣3的图象经过点A（a，1），则a＝.

查看试题解析
4. 在平面直角坐标系中，点 $P (3, - 4)$ 在第象限．

查看试题解析
5. 如图，已知 $△ A B C$ 中， $∠ C = 90 ° ， A D$ 平分 $∠ B A C$ ，且 $C D = 3$ ，则点D到 $A B$ 边的距离为.

查看试题解析
6. 如图， $∠ M O N = 35 °$ ，点P在 $∠ M O N$ 的边 $O N$ 上，以点P为圆心， $P O$ 为半径画弧，交 $O M$ 于点A，连接 $A P$ ，则 $∠ A P N =$ $°$ .

查看试题解析
7. 如图， $B D$ 平分 $∠ A B C ， D E ∥ B C$ 交 $B A$ 于点E，若 $D E = \frac{5}{2}$ ，则 $E B =$ .

查看试题解析
8. 将如图所示的“ $Q Q$ ”笑脸放置在 $3 \times 3$ 的正方形网格中， $A$ 、 $B$ 、 $C$ 三点均在格点上.若 $A$ 、 $B$ 的坐标分别为 $(- 2 ， 1)$ ， $(- 3 ， 2)$ ，则点 $C$ 的坐标为.

查看试题解析
9. 若函数 $y = k x + b$ 的图象经过点 $(0 ， 1)$ ，其图象如图所示，则关于x的不等式 $k x + b > 1$ 的解集为.

查看试题解析
10. 如图，在三角形纸片 $A B C$ 中， $∠ C = 90 ° ， ∠ A = 30 ° ， A C = 9$ ，折叠该纸片，使点C落在 $A B$ 边上的D点处，折痕 $B E$ 与 $A C$ 交于点E，则折痕 $B E$ 的长为.

查看试题解析
11. 如图，在平面直角坐标系中，点 $A (3 ， m)$ 在第一象限，若点A关于x轴的对称点B在直线y=-x+1上，则m的值为.

查看试题解析
12. 如图， $∠ A O B$ 是一角度为 $α$ 的锐角木架，要使木架更加牢固，需在其内部添加一些连接支撑木件 $E F$ 、 $F G$ 、 $G H$ …，且 $O E = E F = F G = G H$ …，在 $O A$ 、 $O B$ 足够长的情况下，如果最多能添加这样的连接支撑木件为6根，则锐角 $α$ 的范围为.

查看试题解析

二、单选题

13. 在下面四个图标（图象）中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
14. 已知点P（1+m，2）在第二象限，则m的取值范围是（）

A、m>-1 B、m<-1 C、m≤-1 D、m≥-1

查看试题解析
15. 有 $5 c m, 13 c m$ 两根木条，现想找一根木条组成直角三角形，则下列木条长度适合的是（）

A、8cm B、12cm C、18cm D、20cm

查看试题解析
16. 已知点A（3，y₁）和点B（﹣2，y₂）是一次函数y＝﹣2x＋3图象上的两点，比较y₁与y₂的大小关系（）

A、y₁＞y₂ B、y₁＝y₂ C、y₁＜y₂ D、不能确定

查看试题解析
17. 如图， $R t △ A O B ≌ R t △ C D A$ ，且点A、B的坐标分别为 $(- 1 ， 0) ， B (0 ， 2)$ ，则 $O D$ 长是（）

A、 $- 3$ B、5 C、4 D、3

查看试题解析
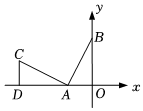18. 如图，在数轴上点B表示的数为1，在点B的右侧作一个边长为1的正方形BACD，将对角线BC绕点B逆时针转动，使对角线的另一端落在数轴负半轴的点M处，则点M表示的数是（）

A、 $\sqrt{2}$ B、 $\sqrt{2}$ +1 C、1﹣ $\sqrt{2}$ D、﹣ $\sqrt{2}$

查看试题解析
19. 如图，边长为5的等边三角形 $A B C$ 中，M是高 $C H$ 所在直线上的一个动点，连接 $M B$ ，将线段 $B M$ 绕点B逆时针旋转 $60 °$ 得到 $B N$ ，连接 $H N$ .则在点M运动过程中，线段 $H N$ 长度的最小值是（）

A、 $\frac{5}{4}$ B、1 C、2 D、 $\frac{5}{2}$

查看试题解析

三、解答题

20. 计算： $\sqrt[3]{- 8} + \sqrt{9} - 2022^{0}$ .

查看试题解析
21. 求下列各式中 $x$ 的值：

(1)、 ${(2 x + 1)}^{2} = 25$ ；

(2)、 $64 x^{3} + 1 = - 26$ .

查看试题解析
22. 如图，点D在 $△ A B C$ 的BC边上， $A C ∥ B E$ ， $B C = B E$ ， $∠ A B C = ∠ E$ .

(1)、求证： $△ A B C ≌ △ D E B$ ；

(2)、若 $B E = 9$ ， $A C = 4$ ，求CD的长，

查看试题解析
23. 如图，在正方形网格中，每个小正方形的边长都为1，点A，点B在网格中的位置如图所示.

(1)、请在下面方格纸中建立适当的平面直角坐标系，使点A、点B的坐标分别为 $(1 ， - 3)$ 、 $(4 ， - 2)$ ；

(2)、点C的坐标为 $(2 ， - 1)$ ，连接 $A B ， B C ， C A$ ，则 $△ A B C$ 的面积为.

(3)、在图中画出 $△ A B C$ 关于y轴对称的图形 $△ A_{1} B_{1} C_{1}$ ；

(4)、在x轴上找到一点P，使 $A P + B P$ 最小，则 $A P + B P$ 的最小值是.

查看试题解析
24. 某地出租车计费方法如图所示， $x (km)$ 表示行驶里程，y（元）表示车费，请根据图象回答下面的问题：

(1)、该地出租车的起步价是元；

(2)、当 $x > 3$ 时，求y关于x的函数关系式；

(3)、若某乘客一次乘出租车的车费为40元，求这位乘客乘车的里程.

查看试题解析
25. 如图， $∠ 1 = ∠ 2$ ， $C E ⊥ A B$ 于E， $C F ⊥ A D$ 交AD的延长线于F，且 $B C = D C$ .

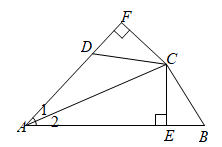(1)、BE与DF是否相等？请说明理由；

(2)、若 $D F = 1 cm$ ， $A D = 3 cm$ ，则AB的长为cm.

查看试题解析
26. 如图，在平面直角坐标系中，直线 $l_{1} ： y = \frac{1}{2} x + b$ 与直线 $l_{2} ： y = 2 x$ 相交于点 $B (m ， 4)$ .

(1)、求m，b的值；

(2)、求 $△ A O B$ 的面积；

(3)、点P是x轴上的一点，过P作垂于x轴的直线与 $l_{1} ， l_{2}$ 的交点分别为C，D，若P点的横坐标为n，当 $C D > 2$ 时直接写出n的取值范围.

查看试题解析
27. 给出如下定义：在平面直角坐标系 $x O y$ 中，已知点 $P_{1} (a ， b) ， P_{2} (c ， b) ， P_{3} (c ， d)$ ，这三个点中任意两点间的距离的最小值称为点 $P_{1} ， P_{2} ， P_{3}$ 的“最短间距”，例如：如图，点 $P_{1} (- 1 ， 2) ， P_{2} (1 ， 2) ， P_{3} (1 ， 3)$ 的“最短间距”是1（即 $P_{2} P_{3}$ 的长）.

(1)、点 $Q_{1} (2 ， 1) ， Q_{2} (4 ， 1) ， Q_{3} (4 ， 4)$ 的最短间距是；

(2)、已知点 $O (0 ， 0) ， A (- 3 ， 0)$ ，点 $B (- 3 ， y)$ 在第三象限.
①若点O，A，B的最短间距是1，求y的值；

②点O，A，B的“最短间距”的最大值为 ▲ ；

(3)、已知直线l与坐标轴分别交于点 $C (0 ， 3)$ 和 $D (4 ， 0)$ ，点 $P (m ， n)$ 是线段 $C D$ 上的一个动点，当点 $O (0 ， 0) ， E (m ， 0) ， P (m ， n)$ 的最短间距取到最大值时，则此时点P的坐标.

查看试题解析