江苏省宿迁市泗洪县2021-2022学年八年级上学期期末数学试卷
试卷更新日期:2022-02-24 类型:期末考试
一、单选题
-
1. 下列四个实数 、π、 、 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个2. 在平面直角坐标系中,点 关于 轴的对称点的坐标是( )A、 B、 C、 D、3. 下列长度的三条线段能组成直角三角形的是( )A、 B、 C、32 , 42 , 52 D、4,5,64. 下列函数中,y是x的正比例函数的是( )A、y=5x﹣1 B、y= x C、y=x2 D、y=5. 关于函数y=-2x+1,下列结论正确的是( )A、图象经过点 B、y随x的增大而增大 C、图象不经过第四象限 D、图象与直线y=-2x平行6.
均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
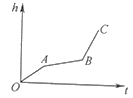 A、
A、 B、
B、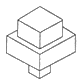 C、
C、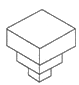 D、
D、 7. 如图是由8个全等的矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA、PB,那么使△ABP为等腰直角三角形的点P的个数是( )
7. 如图是由8个全等的矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA、PB,那么使△ABP为等腰直角三角形的点P的个数是( )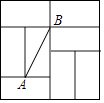 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
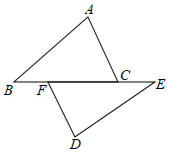
8. 化简: = .9. 点P(﹣5,12)到原点的距离是.10. 小亮的体重为44.85kg,精确到0.1kg得到的近似值为kg.11. 已知一次函数y=x+b的图象经过点A(-1,1),则b的值是.12. 电影票上“10排3号”,记作 ,“8排23号”,记作 ,则“5排16号”记作.13. 如图,△ABC≌△DEF,BE=5,BF=1,则CF=.
 14. 如图,在平面直角坐标系中, , ,以点 为圆心, 长为半径画弧,交 轴的负半轴于点 ,则点 的坐标为 .
14. 如图,在平面直角坐标系中, , ,以点 为圆心, 长为半径画弧,交 轴的负半轴于点 ,则点 的坐标为 .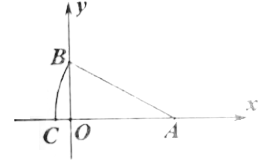 15. 一次函数y=(k+5)x﹣2中y随x的增大而减小,则k的取值范围是.16. 在平面直角坐标系xOy中,一次函数y=kx+b(k≠0,k,b均为常数)与正比例函数y=﹣ x的图象如图所示,则关于x的不等式kx+b>﹣ x的解集为.
15. 一次函数y=(k+5)x﹣2中y随x的增大而减小,则k的取值范围是.16. 在平面直角坐标系xOy中,一次函数y=kx+b(k≠0,k,b均为常数)与正比例函数y=﹣ x的图象如图所示,则关于x的不等式kx+b>﹣ x的解集为. 17. 如图,点阵中的相邻4个顶点的小正方形面积为1,则五边形ABCEF的面积为.
17. 如图,点阵中的相邻4个顶点的小正方形面积为1,则五边形ABCEF的面积为.
三、解答题
-
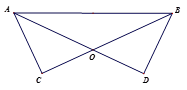
18. 解方程:(1)、 ;(2)、19. 计算: .20. 已知一次函数y=ax-3,当x=1时,y=7,当x=-2时,求y的值.21. 已知:如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.求证:AO=BO.
 22. 如图,四边形ABCD中,∠BAD=∠BCD=90°,BC=CD.
22. 如图,四边形ABCD中,∠BAD=∠BCD=90°,BC=CD. (1)、作图:延长线段AD到点E,使线段DE=AB,连接CE、AC;(2)、求证: ;(3)、求∠BAC的大小.23. 如图,在△ABC中,AB=AC,高BD、CE相于点O.证明OB=OC.
(1)、作图:延长线段AD到点E,使线段DE=AB,连接CE、AC;(2)、求证: ;(3)、求∠BAC的大小.23. 如图,在△ABC中,AB=AC,高BD、CE相于点O.证明OB=OC.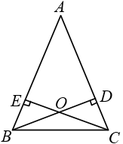 24. “五一节”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
24. “五一节”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象. (1)、求他们出发半小时时,离家多少千米?(2)、求出AB段图象的函数表达式;(3)、他们出发2小时时,离目的地还有多少千米?25. 小明计划购买一双运动鞋,在购物网站上浏览,看到下面的尺码对照表:
(1)、求他们出发半小时时,离家多少千米?(2)、求出AB段图象的函数表达式;(3)、他们出发2小时时,离目的地还有多少千米?25. 小明计划购买一双运动鞋,在购物网站上浏览,看到下面的尺码对照表:中码
220
225
230
…
250
255
260
…
美码
4.5
5
5.5
…
7.5
8
8.5
…
(1)、若小明所穿鞋的中码为245,则对应的美码为;(2)、若美码(y)与中码(x)之间满足一次函数关系,请求出这个函数表达式;(3)、若某篮球运动员的运动鞋美码为18,请求出该运动员运动鞋的中码.26. 如图,已知线段MN=4,点A在线段MN上,且AM=1,点B为线段AN上的一个动点.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,旋转角分别为α和β.若旋转后M、N两点重合成一点C(即构成△ABC),设AB=x. (1)、△ABC的周长为;(2)、若α+β=270°,求x的值;(3)、试探究△ABC是否可能为等腰三角形?若可能,求出x的值;若不可能,请说明理由.27. 【直观想象】如图1,动点P在数轴上从负半轴向正半轴运动,点P到原点的距离先变小再变大,当点P的位置确定时,点P到原点的距离也唯一确定;
(1)、△ABC的周长为;(2)、若α+β=270°,求x的值;(3)、试探究△ABC是否可能为等腰三角形?若可能,求出x的值;若不可能,请说明理由.27. 【直观想象】如图1,动点P在数轴上从负半轴向正半轴运动,点P到原点的距离先变小再变大,当点P的位置确定时,点P到原点的距离也唯一确定;
【数学发现】当一个动点P(x,0)到一个定点的距离为d,我们发现d是x的函数;
【数学理解】动点P(x,0)到定点A(2,0)的距离为d,当x= 时,d取最小值;
【类比迁移】设动点P(x,0)到两个定点M(1,0)、N(3,0)的距离和为y.
①随着x增大,y怎样变化?
②在给出的平面直角坐标系中画出y关于x的函数图象;
③当y>6时,x的取值范围是 .