江苏省连云港市东海县2020-2021学年八年级上学期期末数学试卷
试卷更新日期:2022-02-24 类型:期末考试
一、单选题
-
1. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法正确的是( )A、﹣27的立方根是3 B、 =±4 C、1的平方根是1 D、4的算术平方根是23. 在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为3,到 轴的距离为4,则点 的坐标是( )A、 B、 C、 D、4. 在等腰三角形ABC中,∠A=80°.则∠B的度数不可能为( )A、20° B、40° C、50° D、80°5. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
2. 下列说法正确的是( )A、﹣27的立方根是3 B、 =±4 C、1的平方根是1 D、4的算术平方根是23. 在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为3,到 轴的距离为4,则点 的坐标是( )A、 B、 C、 D、4. 在等腰三角形ABC中,∠A=80°.则∠B的度数不可能为( )A、20° B、40° C、50° D、80°5. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD6. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、7. 李强同学去登山,先匀速登上山顶,原地休息一段时间后,又匀速下山,上山的速度小于下山的速度.在登山过程中,他行走的路程S随时间t的变化规律的大致图象是( )A、 B、
B、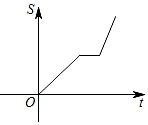 C、
C、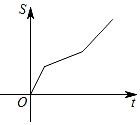 D、
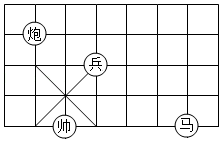
D、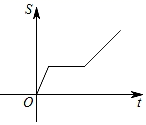 8. 如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC=( )
8. 如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC=( )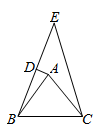 A、90°﹣ m° B、180°﹣2m° C、30°+ m° D、 m°
A、90°﹣ m° B、180°﹣2m° C、30°+ m° D、 m°二、填空题
-
9. 是(填写“有理数”或“无理数”).10. 点P(3,2)关于x轴对称的点的坐标为 .11. 已知变量y与x满足一次函数关系,且y随x的变化而变化,若其图象经过第一、二、三象限,请写出一个满足上述要求的函数关系式.12. 若直角三角形斜边上的高和中线长分别是 , ,则它的面积是 .13. 如图,若在象棋棋盘上建立平面直角坐标系,使“兵”位于点(1,0),“炮”位于点(﹣1,1),则“马”位于点.
 14. 如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组 的解是.
14. 如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组 的解是.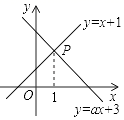 15. 如图的三角形纸片中,AB=7,AC=5,BC=6,沿过点C的直线折叠这个三角形,使点A落在BC边上的点E处,折痕为CD,则△BED的周长为.
15. 如图的三角形纸片中,AB=7,AC=5,BC=6,沿过点C的直线折叠这个三角形,使点A落在BC边上的点E处,折痕为CD,则△BED的周长为.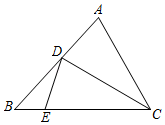 16. 根据教材第65页“思考”栏目可以得到这样一个结论:如图,在Rt△ABC中,∠ACB=90°,∠A=30°,则AB=2BC.请在这一结论的基础上继续思考:若AC=2,点D是AB边上的动点,则CD+ AD的最小值为.
16. 根据教材第65页“思考”栏目可以得到这样一个结论:如图,在Rt△ABC中,∠ACB=90°,∠A=30°,则AB=2BC.请在这一结论的基础上继续思考:若AC=2,点D是AB边上的动点,则CD+ AD的最小值为.
三、解答题
-
17. 解答下列各题:(1)、计算: ﹣ ;(2)、求x的值:2(x﹣1)2﹣18=0.18. 已知y﹣3与2﹣x成正比例,且x=1时y=6.(1)、试求y与x之间的函数表达式;(2)、当y=15时,求x的值.19. 已知:如图,在Rt△ABC中,∠C=90°.
 (1)、做∠A的平分线交BC于点D(要求:尺规作图,保留作图痕迹,不写作法);(2)、若再作∠B的平分线交AD于点P,则∠APB的度数为°.20. 在下面的方格纸中作图:
(1)、做∠A的平分线交BC于点D(要求:尺规作图,保留作图痕迹,不写作法);(2)、若再作∠B的平分线交AD于点P,则∠APB的度数为°.20. 在下面的方格纸中作图: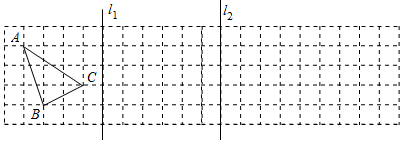 (1)、先画△ABC关于直线l1的对称图形△A1B1C1 , 再画△A1B1C1关于直线l2的对称图形△A2B2C2;(2)、若△ABC向右平移1格,则△A2B2C2向平移格.21. 已知一次函数y=x+3.
(1)、先画△ABC关于直线l1的对称图形△A1B1C1 , 再画△A1B1C1关于直线l2的对称图形△A2B2C2;(2)、若△ABC向右平移1格,则△A2B2C2向平移格.21. 已知一次函数y=x+3. (1)、在如图所示的网格中画该函数的图象;(2)、当0≤x≤6时,y的取值范围是;(3)、当y≥0时,自变量x的取值范围是.22. 如图,直线l经过点A(﹣1,﹣2)和B(0,1).
(1)、在如图所示的网格中画该函数的图象;(2)、当0≤x≤6时,y的取值范围是;(3)、当y≥0时,自变量x的取值范围是.22. 如图,直线l经过点A(﹣1,﹣2)和B(0,1). (1)、求直线l的函数表达式;(2)、线段AB的长为;(3)、在y轴上存在点C,使得以A、B、C为顶点的三角形是以AB为腰的等腰三角形,请直接写出点C的坐标.23. 小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.6m和2m,∠BOC=90°.
(1)、求直线l的函数表达式;(2)、线段AB的长为;(3)、在y轴上存在点C,使得以A、B、C为顶点的三角形是以AB为腰的等腰三角形,请直接写出点C的坐标.23. 小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.6m和2m,∠BOC=90°.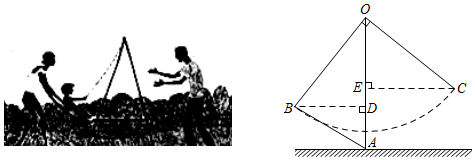 (1)、△OBD与△COE全等吗?请说明理由;(2)、爸爸是在距离地面多高的地方接住小明的?24. 如图,公路上有A、B、C三个汽车站,一辆汽车8:00从离C站340km的A站出发,向C站匀速行驶,15min后离C站320km.
(1)、△OBD与△COE全等吗?请说明理由;(2)、爸爸是在距离地面多高的地方接住小明的?24. 如图,公路上有A、B、C三个汽车站,一辆汽车8:00从离C站340km的A站出发,向C站匀速行驶,15min后离C站320km. (1)、设出发xh后,汽车离C站ykm,则y与x之间的函数表达式为;(2)、当汽车行驶到离C站还有100km的B站时,司机接到通知要在12:00前赶到离C站190km的服务区P(在A、B之间).汽车按原速行驶,能否准时到达?说明理由.25. 问题情境:
(1)、设出发xh后,汽车离C站ykm,则y与x之间的函数表达式为;(2)、当汽车行驶到离C站还有100km的B站时,司机接到通知要在12:00前赶到离C站190km的服务区P(在A、B之间).汽车按原速行驶,能否准时到达?说明理由.25. 问题情境:七下教材第149页提出这样一个问题:如图1,∠AOB=90°,OC平分∠AOB,把三角尺的直角顶点落在OC的任意一点P上,并使三角尺的两条直角边分别与OA、OB相交于点E、F,PE与PF相等吗?
 (1)、七年级学习这部分内容时,我们还无法对这个问题的结论加以证明,八下教材第59页第11题不仅对这一问题给出了答案:“通过实验可以得到PE=PF”,还要求“现在请你证明这个结论”,请你给出证明:(2)、变式拓展:
(1)、七年级学习这部分内容时,我们还无法对这个问题的结论加以证明,八下教材第59页第11题不仅对这一问题给出了答案:“通过实验可以得到PE=PF”,还要求“现在请你证明这个结论”,请你给出证明:(2)、变式拓展:
如图2,已知∠AOB=120°,OC平分∠AOB,P是OC上一点,∠EPF=60°,PE边与OA边相交于点E,PF边与射线OB的反向延长线相交于点F.试解决下列问题:①PE与PF还相等吗?为什么?
②试判断OE、OF、OP三条线段之间的数量关系,并说明理由.
26. 如图1,一次函数y= x+4的图象与x轴、y轴分别交于点A、B.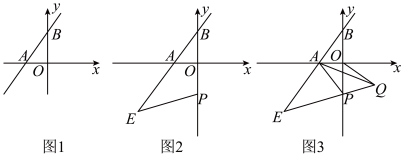 (1)、则点A的坐标为 , 点B的坐标为;(2)、如图2,点P为y轴上的动点,以点P为圆心,PB长为半径画弧,与BA的延长线交于点E,连接PE,已知PB=PE,求证:∠BPE=2∠OAB;(3)、在(2)的条件下,如图3,连接PA,以PA为腰作等腰三角形PAQ,其中PA=PQ,∠APQ=2∠OAB.连接OQ.
(1)、则点A的坐标为 , 点B的坐标为;(2)、如图2,点P为y轴上的动点,以点P为圆心,PB长为半径画弧,与BA的延长线交于点E,连接PE,已知PB=PE,求证:∠BPE=2∠OAB;(3)、在(2)的条件下,如图3,连接PA,以PA为腰作等腰三角形PAQ,其中PA=PQ,∠APQ=2∠OAB.连接OQ.①则图中(不添加其他辅助线)与∠EPA相等的角有 ;(都写出来)
②试求线段OQ长的最小值.